Lab: Classification Methods¶
The Stock Market Data¶
We will begin by examining some numerical and graphical summaries of
the Smarket data, which is part of the ISLR2 library. This
data set consists of percentage returns for the S\&P 500 stock index
over $1,250$~days, from the beginning of 2001 until the end of
- For each date, we have recorded the percentage returns for each
of the five previous trading days,
lagonethroughlagfive. We have also recordedvolume(the number of shares traded on the previous day, in billions),Today(the percentage return on the date in question) anddirection(whether the market wasUporDownon this date). Our goal is to predictdirection(a qualitative response) using the other features.
library(ISLR2)
names(Smarket)
dim(Smarket)
summary(Smarket)
pairs(Smarket)
The cor() function produces a matrix that contains all of the pairwise correlations among the predictors in a data set. The first command below gives an error message because the direction variable is qualitative.
cor(Smarket)
cor(Smarket[, -9])
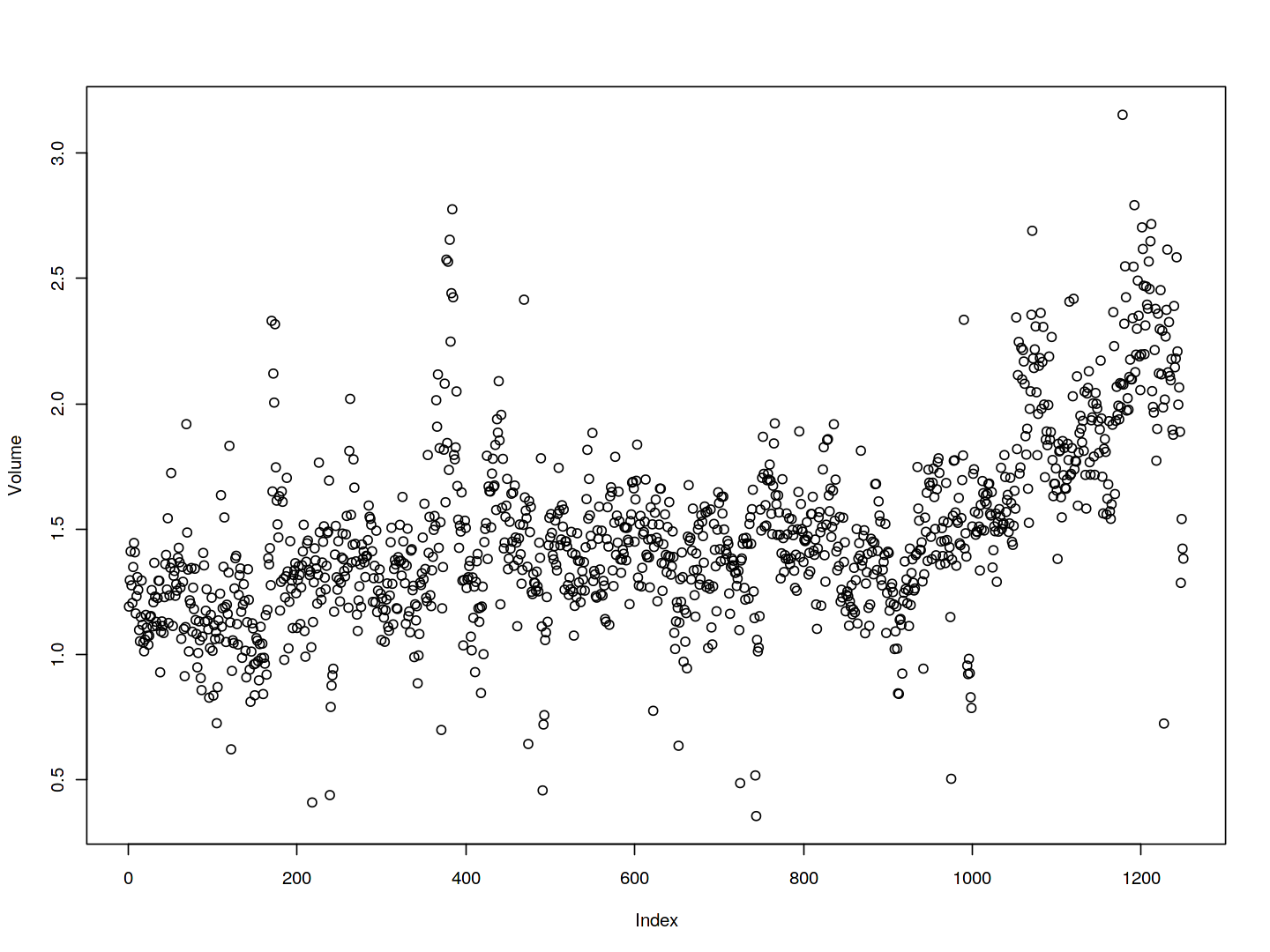
As one would expect, the correlations between the lag variables and today's returns are close to zero. In other words, there appears to be little correlation between today's returns and previous days' returns. The only substantial correlation is between Year and volume. By plotting the data, which is ordered chronologically, we see that volume is increasing over time. In other words, the average number of shares traded daily increased from 2001 to 2005.
attach(Smarket)
plot(Volume)
Logistic Regression¶
Next, we will fit a logistic regression model in order to predict direction using lagone through lagfive and volume. The glm() function can be used to fit many types of generalized linear models , including logistic regression.
The syntax of the glm() function is similar to that of lm(), except that we must pass in the argument family = binomial in order to tell R to run a logistic regression rather than some other type of generalized linear model.
glm.fits <- glm(
Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data = Smarket, family = binomial
)
summary(glm.fits)
The smallest $p$-value here is associated with lagone. The negative coefficient for this predictor suggests that if the market had a positive return yesterday, then it is less likely to go up today. However, at a value of $0.15$, the $p$-value is still relatively large, and so there is no clear evidence of a real association between lagone and direction.
We use the coef() function in order to access just the coefficients for this fitted model. We can also use the summary() function to access particular aspects of the fitted model, such as the $p$-values for the coefficients.
coef(glm.fits)
summary(glm.fits)$coef
summary(glm.fits)$coef[, 4]
The predict() function can be used to predict the probability that the market will go up, given values of the predictors. The type = "response" option tells R to output probabilities of the form $P(Y=1|X)$, as opposed to other information such as the logit. If no data set is supplied to the predict() function,
then the probabilities are computed for the training data that was used to fit the logistic regression model. Here we have printed only the first ten probabilities. We know that these values correspond to the probability of the market going up, rather than down, because the contrasts() function indicates that R has created a dummy variable with a 1 for Up.
glm.probs <- predict(glm.fits, type = "response")
glm.probs[1:10]
contrasts(Direction)
In order to make a prediction as to whether the market will go up or down on a particular day, we must convert these predicted probabilities into class labels, Up or Down.
The following two commands create a vector of class predictions based on whether the predicted probability of a market increase is greater than or less than $0.5$.
glm.pred <- rep("Down", 1250)
glm.pred[glm.probs > .5] = "Up"
The first command creates a vector of 1,250 Down elements. The second line transforms to Up all of the elements for which the predicted probability of a market increase exceeds $0.5$. Given these predictions, the table() function can be used to produce a confusion matrix in order to determine how many observations were correctly or incorrectly classified. %By inputting two qualitative vectors R will create a two by two table with counts of the number of times each combination occurred e.g. predicted {\it Up} and market increased, predicted {\it Up} and the market decreased etc.
table(glm.pred, Direction)
(507 + 145) / 1250
mean(glm.pred == Direction)
The diagonal elements of the confusion matrix indicate correct predictions, while the off-diagonals represent incorrect predictions. Hence our model correctly predicted that the market would go up on $507$~days and that it would go down on $145$~days, for a total of $507+145 = 652$ correct predictions. The mean() function can be used to compute the fraction of days for which the prediction was correct. In this case, logistic regression correctly predicted the movement of the market $52.2$\,\% of the time.
At first glance, it appears that the logistic regression model is working a little better than random guessing. However, this result is misleading because we trained and tested the model on the same set of $1,250$ observations. In other words, $100\%-52.2\%=47.8\%$, is the training error rate. As we have seen previously, the training error rate is often overly optimistic---it tends to underestimate the test error rate. In order to better assess the accuracy of the logistic regression model in this setting, we can fit the model using part of the data, and then examine how well it predicts the held out data. This will yield a more realistic error rate, in the sense that in practice we will be interested in our model's performance not on the data that we used to fit the model, but rather on days in the future for which the market's movements are unknown.
To implement this strategy, we will first create a vector corresponding to the observations from 2001 through 2004. We will then use this vector to create a held out data set of observations from 2005.
train <- (Year < 2005)
Smarket.2005 <- Smarket[!train, ]
dim(Smarket.2005)
Direction.2005 <- Direction[!train]
The object train is a vector of $1{,}250$ elements, corresponding to the observations in our data set. The elements of the vector that correspond to observations that occurred before 2005 are set to TRUE, whereas those that correspond to observations in 2005 are set to FALSE.
The object train is a Boolean vector, since its elements are TRUE and FALSE.
Boolean vectors can be used to obtain a subset of the rows or columns of a matrix. For instance, the command Smarket[train, ] would pick out a submatrix of the stock market data set, corresponding only to the dates before 2005, since
those are the ones for which the elements of train are TRUE.
The ! symbol can be used to reverse all of the elements of a Boolean vector. That is, !train is a vector similar to train, except that the elements that are TRUE in train get swapped to FALSE in !train, and the elements that are FALSE
in train get swapped to TRUE in !train. Therefore, Smarket[!train, ] yields a submatrix of the stock market data containing only
the observations for which train is FALSE---that is, the observations with dates in 2005. The output above indicates that there are 252 such observations.
We now fit a logistic regression model using only the subset of the observations that correspond to dates before 2005, using the subset argument. We then obtain predicted probabilities of the stock market going up for each of the days in our test set---that is, for the days in 2005.
glm.fits <- glm(
Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data = Smarket, family = binomial, subset = train
)
glm.probs <- predict(glm.fits, Smarket.2005,
type = "response")
Notice that we have trained and tested our model on two completely separate data sets: training was performed using only the dates before 2005, and testing was performed using only the dates in 2005. Finally, we compute the predictions for 2005 and compare them to the actual movements of the market over that time period.
glm.pred <- rep("Down", 252)
glm.pred[glm.probs > .5] <- "Up"
table(glm.pred, Direction.2005)
mean(glm.pred == Direction.2005)
mean(glm.pred != Direction.2005)
The != notation means not equal to, and so the last command computes the test set error rate. The results are rather disappointing: the test error rate is $52$\,\%, which is worse than random guessing! Of course this result is not all that surprising, given that one would not generally expect to be able to use previous days' returns to predict future market performance. (After all, if it were possible to do so, then the authors of this book would be out striking it rich rather than writing a statistics textbook.)
We recall that the logistic regression model had very underwhelming $p$-values associated with all of the predictors, and that the smallest $p$-value, though not very small, corresponded to lagone. Perhaps by removing the variables that appear not to be helpful in
predicting
direction, we can obtain a more effective model. After all, using predictors that have no relationship with the response tends to cause a deterioration in the test error rate (since such predictors cause an increase in variance without a corresponding decrease in bias), and so removing such predictors may in turn yield an improvement.
Below we have refit the logistic regression using just lagone and lagtwo, which seemed to have the highest predictive power in the original logistic regression model.
glm.fits <- glm(Direction ~ Lag1 + Lag2, data = Smarket,
family = binomial, subset = train)
glm.probs <- predict(glm.fits, Smarket.2005,
type = "response")
glm.pred <- rep("Down", 252)
glm.pred[glm.probs > .5] <- "Up"
table(glm.pred, Direction.2005)
mean(glm.pred == Direction.2005)
106 / (106 + 76)
Now the results appear to be a little better: $56\%$ of the daily movements have been correctly predicted. It is worth noting that in this case, a much simpler strategy of predicting that the market will increase every day will also be correct $56\%$ of the time! Hence, in terms of overall error rate, the logistic regression method is no better than the naive approach. However, the confusion matrix shows that on days when logistic regression predicts an increase in the market, it has a $58\%$ accuracy rate. This suggests a possible trading strategy of buying on days when the model predicts an increasing market, and avoiding trades on days when a decrease is predicted. Of course one would need to investigate more carefully whether this small improvement was real or just due to random chance.
Suppose that we want to predict the returns associated with particular values of lagone and lagtwo. In particular, we want to predict direction on a day when lagone and lagtwo equal 1.2 and~1.1, respectively, and on a day when they equal 1.5 and $-$0.8.
We do this using the predict() function.
predict(glm.fits,
newdata =
data.frame(Lag1 = c(1.2, 1.5), Lag2 = c(1.1, -0.8)),
type = "response"
)
Linear Discriminant Analysis¶
Now we will perform LDA on the Smarket data. In R, we fit an LDA model using the lda() function, which is part of the MASS library. Notice that the syntax for the lda() function is identical to that of lm(), and to that of glm() except for the absence of the family option. We fit the model using only the observations before 2005.
library(MASS)
lda.fit <- lda(Direction ~ Lag1 + Lag2, data = Smarket,
subset = train)
lda.fit
plot(lda.fit)
The LDA output indicates that $\hat\pi_1=0.492$ and $\hat\pi_2=0.508$; in other words, $49.2$\,\% of the training observations correspond to days during which the market went down.
It also provides the group means; these are the average of each predictor within each class, and are used by LDA as estimates of $\mu_k$.
These suggest that there is a tendency for the previous 2~days' returns to be negative on days when the market increases, and a tendency for the previous days' returns to be positive on days when the market declines.
The coefficients of linear discriminants output provides the linear combination of lagone and lagtwo that are used to form the LDA decision rule. In other words, these are the multipliers of the elements of $X=x$ in ( 4.24).
If $-0.642\times `lagone` - 0.514 \times `lagtwo`$ is large, then the LDA classifier will predict a market increase, and if it is small, then the LDA classifier will predict a market decline.
The plot() function produces plots of the linear discriminants, obtained by computing $-0.642\times `lagone` - 0.514 \times `lagtwo`$ for each of the training observations. The Up and Down observations are displayed separately.
The predict() function returns a list with three elements. The first element, class, contains LDA's predictions about the movement of the market. The second element, posterior, is a matrix whose $k$th column contains the posterior probability that the corresponding observation belongs to the $k$th class, computed from ( 4.15). Finally, x contains the linear discriminants, described earlier.
lda.pred <- predict(lda.fit, Smarket.2005)
names(lda.pred)
As we observed in Section 4.5, the LDA and logistic regression predictions are almost identical.
lda.class <- lda.pred$class
table(lda.class, Direction.2005)
mean(lda.class == Direction.2005)
Applying a $50$\,\% threshold to the posterior probabilities allows us to recreate the predictions contained in lda.pred$class.
sum(lda.pred$posterior[, 1] >= .5)
sum(lda.pred$posterior[, 1] < .5)
Notice that the posterior probability output by the model corresponds to the probability that the market will decrease:
lda.pred$posterior[1:20, 1]
lda.class[1:20]
If we wanted to use a posterior probability threshold other than $50$\,\% in order to make predictions, then we could easily do so. For instance, suppose that we wish to predict a market decrease only if we are very certain that the market will indeed decrease on that day---say, if the posterior probability is at least $90$\,\%.
sum(lda.pred$posterior[, 1] > .9)
No days in 2005 meet that threshold! In fact, the greatest posterior probability of decrease in all of 2005 was $52.02$\,\%.
Quadratic Discriminant Analysis¶
We will now fit a QDA model to the Smarket data. QDA is implemented in R using the qda() function, which is also part of the MASS library. The syntax is identical to that of lda().
qda.fit <- qda(Direction ~ Lag1 + Lag2, data = Smarket,
subset = train)
qda.fit
The output contains the group means. But it does not contain the coefficients of the linear discriminants, because the QDA classifier involves a quadratic, rather than a linear, function of the predictors. The predict() function works in exactly the same fashion as for LDA.
qda.class <- predict(qda.fit, Smarket.2005)$class
table(qda.class, Direction.2005)
mean(qda.class == Direction.2005)
Interestingly, the QDA predictions are accurate almost $60$\,\% of the time, even though the 2005 data was not used to fit the model. This level of accuracy is quite impressive for stock market data, which is known to be quite hard to model accurately. This suggests that the quadratic form assumed by QDA may capture the true relationship more accurately than the linear forms assumed by LDA and logistic regression. However, we recommend evaluating this method's performance on a larger test set before betting that this approach will consistently beat the market!
Naive Bayes¶
Next, we fit a naive Bayes model to the Smarket data. Naive Bayes is implemented in R using the naiveBayes() function, which is part of the e1071 library. The syntax is identical to that of lda() and qda().
By default, this implementation of the naive Bayes classifier models each quantitative feature using a Gaussian distribution. However, a kernel density method can also be used to estimate the distributions.
library(e1071)
nb.fit <- naiveBayes(Direction ~ Lag1 + Lag2, data = Smarket,
subset = train)
nb.fit
The output contains the estimated mean and standard deviation for each variable in each class. For example, the mean for lagone is $0.0428$ for
Direction=Down, and the standard deviation is $1.23$. We can easily verify this:
mean(Lag1[train][Direction[train] == "Down"])
sd(Lag1[train][Direction[train] == "Down"])
The predict() function is straightforward.
nb.class <- predict(nb.fit, Smarket.2005)
table(nb.class, Direction.2005)
mean(nb.class == Direction.2005)
Naive Bayes performs very well on this data, with accurate predictions over $59\%$ of the time. This is slightly worse than QDA, but much better than LDA.
The predict() function can also generate estimates of the probability that each observation belongs to a particular class. %
nb.preds <- predict(nb.fit, Smarket.2005, type = "raw")
nb.preds[1:5, ]
$K$-Nearest Neighbors¶
We will now perform KNN using the knn() function, which is part of the class library. This function works rather differently from the other model-fitting functions that we have encountered thus far.
Rather than a two-step approach in which we first fit the model and then we use the model to make predictions, knn() forms predictions using a single command. The function requires four inputs.
- A matrix containing the predictors associated with the training data, labeled
train.Xbelow. - A matrix containing the predictors associated with the data for which we wish to make predictions, labeled
test.Xbelow. - A vector containing the class labels for the training observations, labeled
train.Directionbelow. - A value for $K$, the number of nearest neighbors to be used by the classifier.
We use the cbind() function, short for column bind, to bind the lagone and lagtwo variables together into two matrices, one for the training set and the other for the test set.
library(class)
train.X <- cbind(Lag1, Lag2)[train, ]
test.X <- cbind(Lag1, Lag2)[!train, ]
train.Direction <- Direction[train]
Now the knn() function can be used to predict the market's movement for the dates in 2005. We set a random seed before we apply knn() because if several observations are tied as nearest neighbors, then R will randomly break the tie. Therefore, a seed must be set in order to ensure reproducibility of results.
set.seed(1)
knn.pred <- knn(train.X, test.X, train.Direction, k = 1)
table(knn.pred, Direction.2005)
(83 + 43) / 252
The results using $K=1$ are not very good, since only $50$\,\% of the observations are correctly predicted. Of course, it may be that $K=1$ results in an overly flexible fit to the data. Below, we repeat the analysis using $K=3$.
knn.pred <- knn(train.X, test.X, train.Direction, k = 3)
table(knn.pred, Direction.2005)
mean(knn.pred == Direction.2005)
The results have improved slightly. But increasing $K$ further turns out to provide no further improvements. It appears that for this data, QDA provides the best results of the methods that we have examined so far.
KNN does not perform well on the Smarket data but it does often provide impressive results. As an example we will apply the KNN approach to the Insurance data set, which is part of the ISLR2 library. This data set includes $85$ predictors that measure
demographic characteristics for 5,822 individuals. The response variable is Purchase, which indicates whether or not a given individual purchases a caravan insurance policy. In this data set, only $6$\,\% of people purchased caravan insurance.
dim(Caravan)
attach(Caravan)
summary(Purchase)
348 / 5822
Because the KNN classifier predicts the class of a given test observation by identifying the observations that are nearest to it, the scale of the variables matters. Variables that are on a large scale will have a much larger effect
on the distance between the observations, and hence
on the KNN classifier, than variables that are on a small scale. For instance, imagine a data set that contains two variables, salary and age (measured in dollars and years, respectively). As far as KNN is concerned, a difference of $1,000 in salary is enormous compared to a difference of $50$~years in age. Consequently, `salary` will drive the KNN classification results, and `age` will have almost no effect. This is contrary to our intuition that a salary difference of $$1{,}000$ is quite small compared to an age difference of $50$~years.
Furthermore, the importance of scale to the KNN classifier leads to another issue: if we measured salary in Japanese yen, or if we measured age in minutes, then we'd get quite different classification results from what we get
if these two variables are measured in dollars and years.
A good way to handle this problem is to the data so that all variables are given a mean of zero and a standard deviation of one. Then all variables will be on a comparable scale. The scale() function does just this.
In standardizing the data, we exclude column $86$, because that is the qualitative Purchase variable.
standardized.X <- scale(Caravan[, -86])
var(Caravan[, 1])
var(Caravan[, 2])
var(standardized.X[, 1])
var(standardized.X[, 2])
Now every column of standardized.X has a standard deviation of one and a mean of zero.
We now split the observations into a test set, containing the first 1,000 observations, and a training set, containing the remaining observations. We fit a KNN model on the training data using $K=1$, and evaluate its performance on the test data.%
test <- 1:1000
train.X <- standardized.X[-test, ]
test.X <- standardized.X[test, ]
train.Y <- Purchase[-test]
test.Y <- Purchase[test]
set.seed(1)
knn.pred <- knn(train.X, test.X, train.Y, k = 1)
mean(test.Y != knn.pred)
mean(test.Y != "No")
The vector test is numeric, with values
from $1$ through $1,000$. Typing standardized.X[test, ] yields the submatrix of the data containing the observations whose indices range from $1$ to $1,000$, whereas typing
standardized.X[-test, ] yields the submatrix containing the observations whose indices do
not range from $1$ to $1,000$.
The KNN error rate on the 1,000 test observations is just under $12$\,\%. At first glance, this may appear to be fairly good. However, since only $6$\,\% of customers purchased insurance, we could get the error rate down to $6$\,\% by always predicting No regardless of
the values of the predictors!
Suppose that there is some non-trivial cost to trying to sell insurance to a given individual. For instance, perhaps a salesperson must visit each potential customer. If the company tries to sell insurance to a random selection of customers, then the success rate will be only $6$\,\%, which may be far too low given the costs involved. Instead, the company would like to try to sell insurance only to customers who are likely to buy it. So the overall error rate is not of interest. Instead, the fraction of individuals that are correctly predicted to buy insurance is of interest.
It turns out that KNN with $K=1$ does far better than random guessing among the customers that are predicted to buy insurance. Among $77$ such customers, $9$, or $11.7$\,\%, actually do purchase insurance. This is double the rate that one would obtain from random guessing.
table(knn.pred, test.Y)
9 / (68 + 9)
Using $K=3$, the success rate increases to $19$\,\%, and with $K=5$ the rate is $26.7$\,\%. This is over four times the rate that results from random guessing. It appears that KNN is finding some real patterns in a difficult data set!
knn.pred <- knn(train.X, test.X, train.Y, k = 3)
table(knn.pred, test.Y)
5 / 26
knn.pred <- knn(train.X, test.X, train.Y, k = 5)
table(knn.pred, test.Y)
4 / 15
However, while this strategy is cost-effective, it is worth noting that only 15 customers are predicted to purchase insurance using KNN with $K=5$. In practice, the insurance company may wish to expend resources on convincing more than just 15 potential customers to buy insurance.
As a comparison, we can also fit a logistic regression model to the data. If we use $0.5$ as the predicted probability cut-off for the classifier, then we have a problem: only seven of the test observations are predicted to purchase insurance. Even worse, we are wrong about all of these! However, we are not required to use a cut-off of $0.5$. If we instead predict a purchase any time the predicted probability of purchase exceeds $0.25$, we get much better results: we predict that 33 people will purchase insurance, and we are correct for about $33$\,\% of these people. This is over five times better than random guessing!
glm.fits <- glm(Purchase ~ ., data = Caravan,
family = binomial, subset = -test)
glm.probs <- predict(glm.fits, Caravan[test, ],
type = "response")
glm.pred <- rep("No", 1000)
glm.pred[glm.probs > .5] <- "Yes"
table(glm.pred, test.Y)
glm.pred <- rep("No", 1000)
glm.pred[glm.probs > .25] <- "Yes"
table(glm.pred, test.Y)
11 / (22 + 11)
Poisson Regression¶
Finally, we fit a Poisson regression model to the Bikeshare data set, which measures the number of bike rentals (bikers) per hour in Washington, DC. The data can be found in the ISLR2 library.
attach(Bikeshare)
dim(Bikeshare)
names(Bikeshare)
We begin by fitting a least squares linear regression model to the data.
mod.lm <- lm(
bikers ~ mnth + hr + workingday + temp + weathersit,
data = Bikeshare
)
summary(mod.lm)
Due to space constraints, we truncate the output of summary(mod.lm).
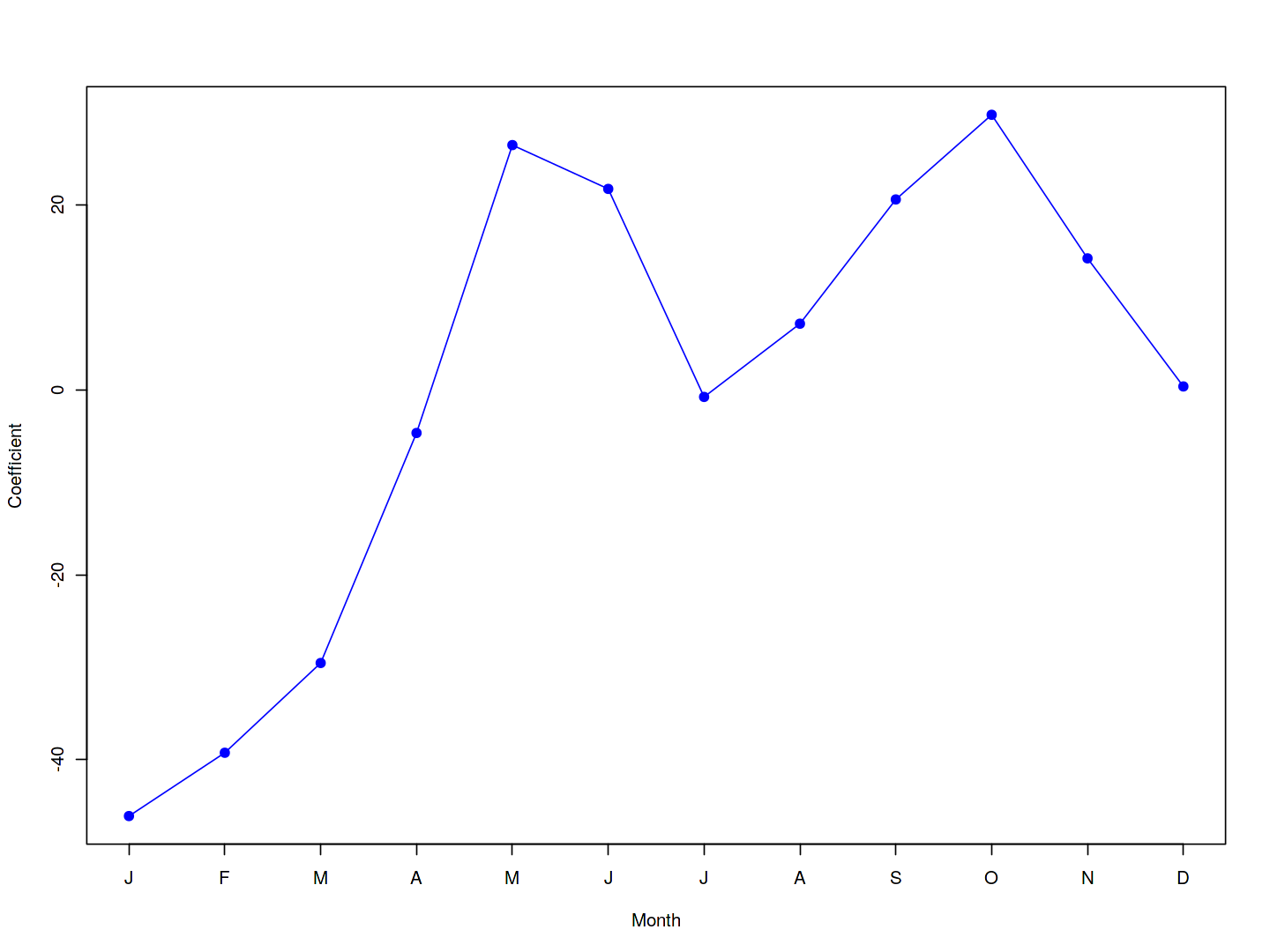
In mod.lm, the first level of hr (0) and mnth (Jan) are treated as the baseline values, and so no coefficient estimates are provided for them: implicitly, their coefficient estimates are zero, and all other levels are measured relative to these baselines. For example, the Feb coefficient of $6.845$ signifies that, holding all other variables constant, there are on average about 7 more riders in February than in January. Similarly there are about 16.5 more riders in March than in January.
The results seen in Section 4.6.1 used a slightly different coding of the variables hr and mnth, as follows:
contrasts(Bikeshare$hr) = contr.sum(24)
contrasts(Bikeshare$mnth) = contr.sum(12)
mod.lm2 <- lm(
bikers ~ mnth + hr + workingday + temp + weathersit,
data = Bikeshare
)
summary(mod.lm2)
What is the difference between the two codings? In mod.lm2, a coefficient estimate is reported for all but the last level of hr and mnth. Importantly, in mod.lm2, the coefficient estimate for the last level of mnth is not zero: instead, it equals the negative of the sum of the coefficient estimates for all of the other levels. Similarly, in mod.lm2, the coefficient estimate for the last level of hr is the negative of the sum of the coefficient estimates for all of the other levels. This means that the coefficients of hr and mnth in mod.lm2 will always sum to zero, and can be interpreted as the difference from the mean level. For example, the coefficient for January of $-46.087$ indicates that, holding all other variables constant, there are typically 46 fewer riders in January relative to the yearly average.
It is important to realize that the choice of coding really does not matter, provided that we interpret the model output correctly in light of the coding used. For example, we see that the predictions from the linear model are the same regardless of coding:
sum((predict(mod.lm) - predict(mod.lm2))^2)
The sum of squared differences is zero. We can also see this using the all.equal() function:
all.equal(predict(mod.lm), predict(mod.lm2))
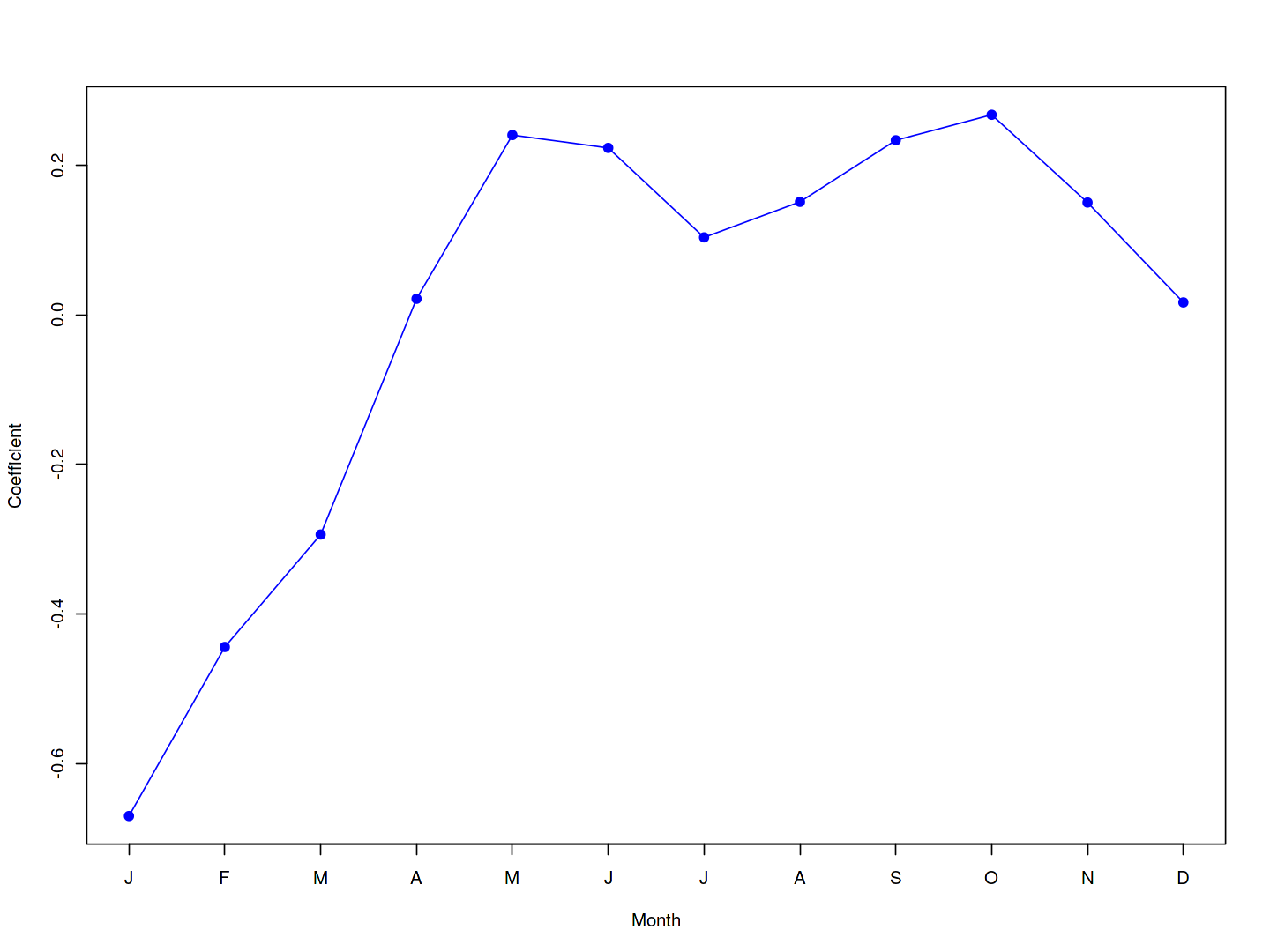
To reproduce the left-hand side of Figure 4.13, we must first obtain the coefficient estimates associated with mnth. The coefficients for January through November can be obtained directly from the mod.lm2 object. The coefficient for December must be explicitly computed as the negative sum of all the other months.
coef.months <- c(coef(mod.lm2)[2:12],
-sum(coef(mod.lm2)[2:12]))
To make the plot, we manually label the $x$-axis with the names of the months.
plot(coef.months, xlab = "Month", ylab = "Coefficient",
xaxt = "n", col = "blue", pch = 19, type = "o")
axis(side = 1, at = 1:12, labels = c("J", "F", "M", "A",
"M", "J", "J", "A", "S", "O", "N", "D"))
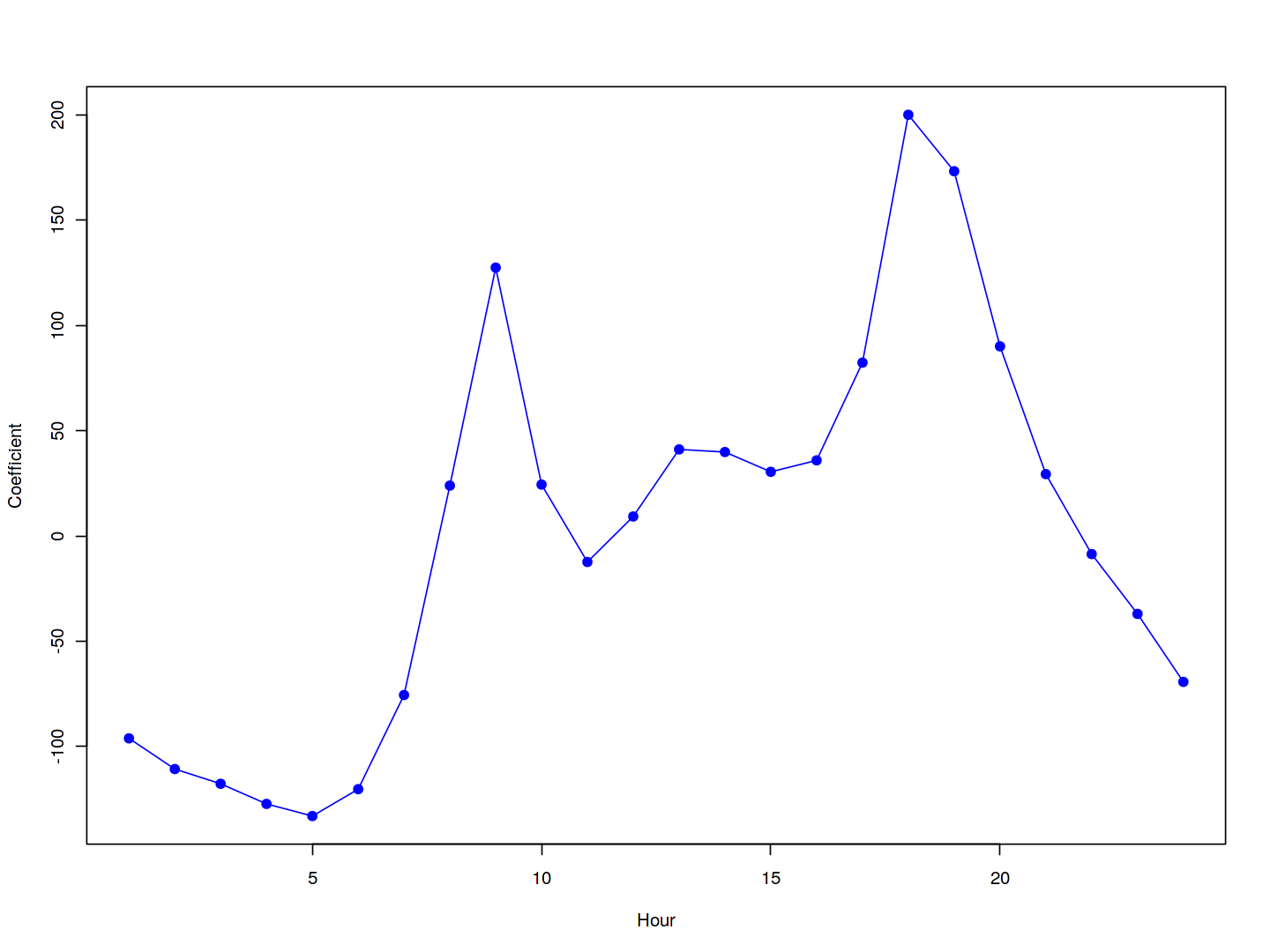
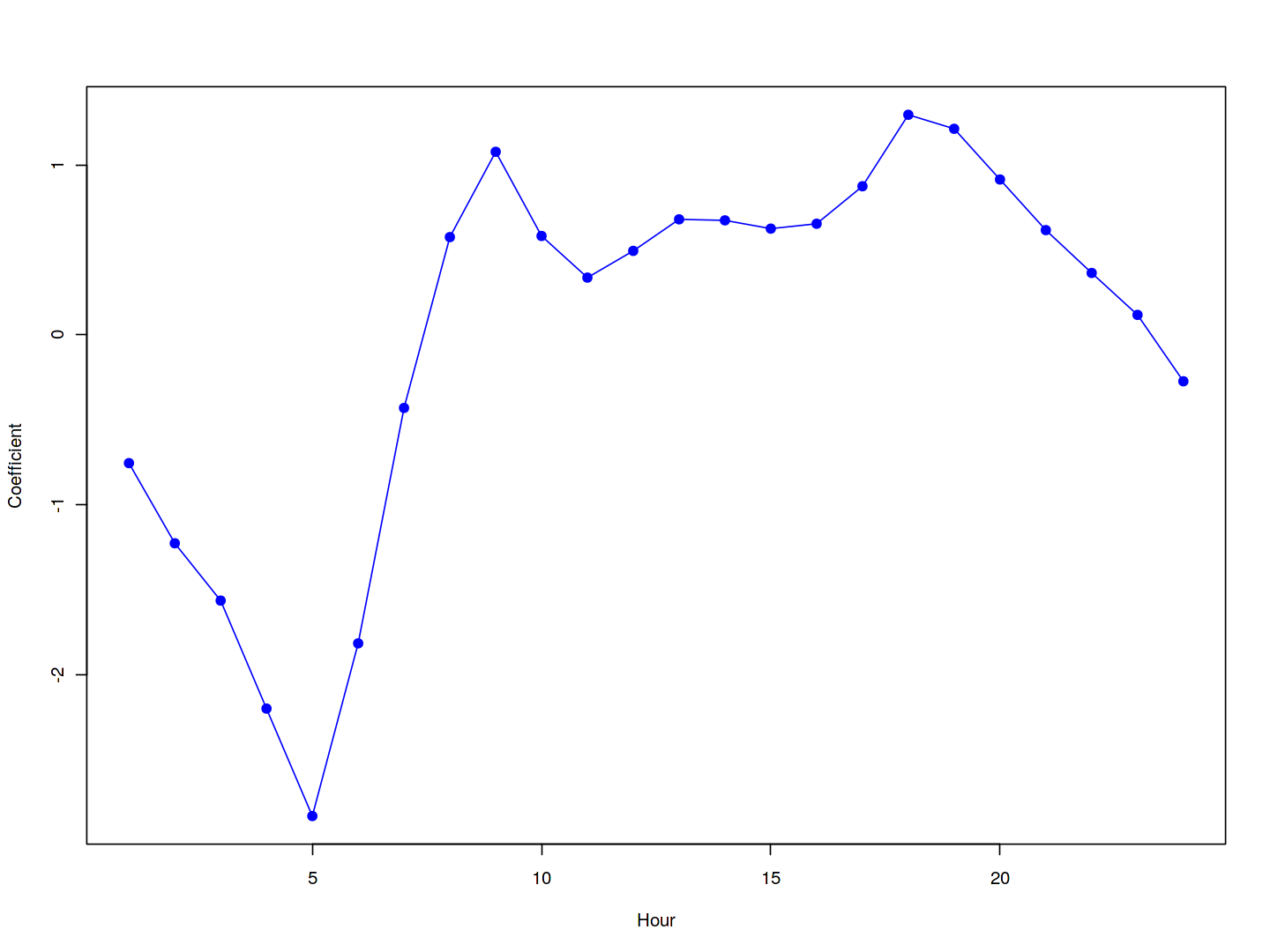
Reproducing the right-hand side of Figure 4.13 follows a similar process.
coef.hours <- c(coef(mod.lm2)[13:35],
-sum(coef(mod.lm2)[13:35]))
plot(coef.hours, xlab = "Hour", ylab = "Coefficient",
col = "blue", pch = 19, type = "o")
Now, we consider instead fitting a Poisson regression model to the Bikeshare data. Very little changes, except that we now use the function glm() with the argument family = poisson to specify that we wish to fit a Poisson regression model:
mod.pois <- glm(
bikers ~ mnth + hr + workingday + temp + weathersit,
data = Bikeshare, family = poisson
)
summary(mod.pois)
We can plot the coefficients associated with mnth and hr, in order to reproduce Figure 4.15:
coef.mnth <- c(coef(mod.pois)[2:12],
-sum(coef(mod.pois)[2:12]))
plot(coef.mnth, xlab = "Month", ylab = "Coefficient",
xaxt = "n", col = "blue", pch = 19, type = "o")
axis(side = 1, at = 1:12, labels = c("J", "F", "M", "A", "M", "J", "J", "A", "S", "O", "N", "D"))
coef.hours <- c(coef(mod.pois)[13:35],
-sum(coef(mod.pois)[13:35]))
plot(coef.hours, xlab = "Hour", ylab = "Coefficient",
col = "blue", pch = 19, type = "o")
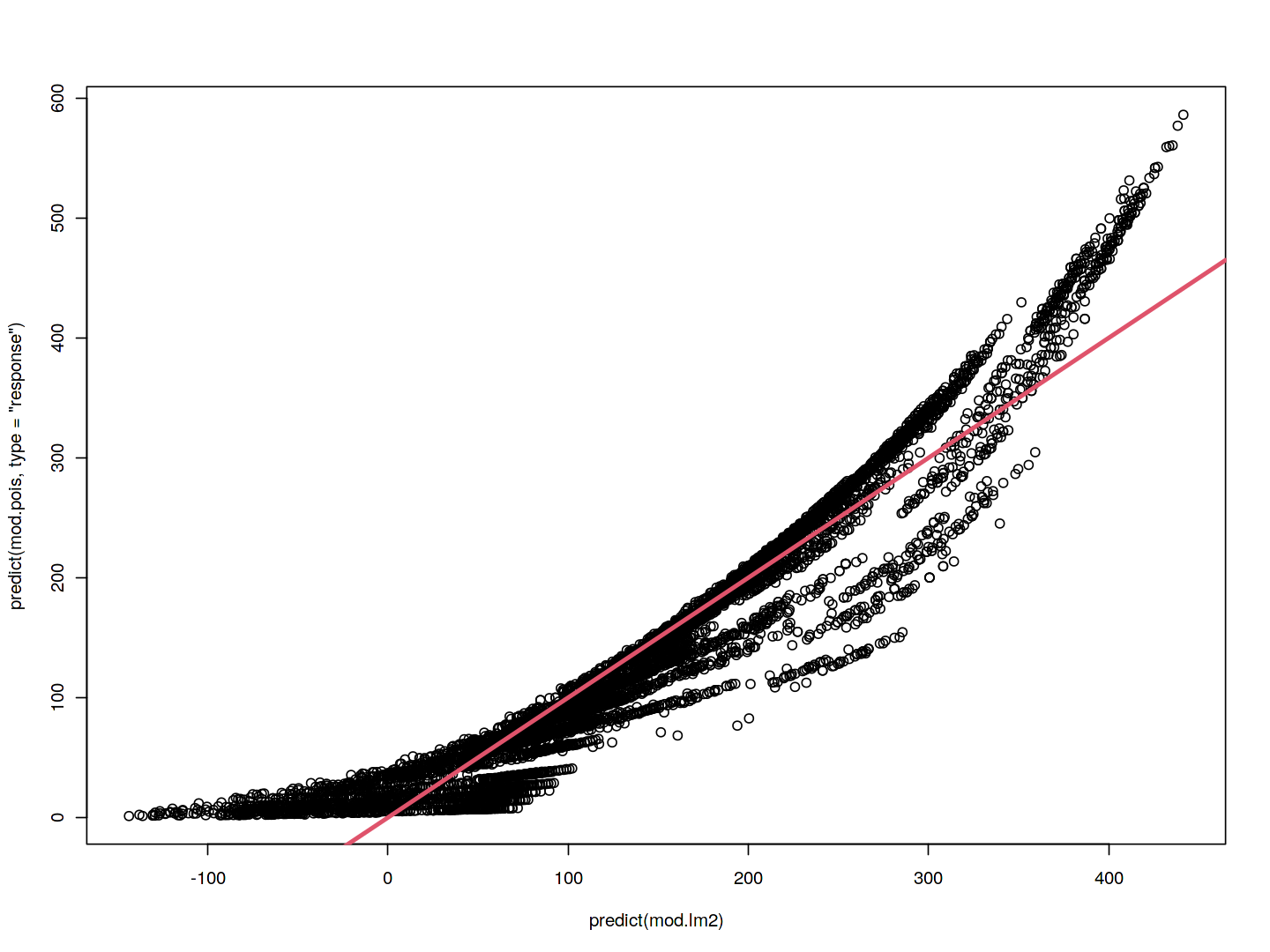
We can once again use the predict() function to obtain the fitted values (predictions) from this Poisson regression model. However, we must use the argument type = "response" to specify that we want R to output $\exp(\hat\beta_0 + \hat\beta_1 X_1 + \ldots +\hat\beta_p X_p)$ rather than $\hat\beta_0 + \hat\beta_1 X_1 + \ldots + \hat\beta_p X_p$, which it will output by default.
plot(predict(mod.lm2), predict(mod.pois, type = "response"))
abline(0, 1, col = 2, lwd = 3)
The predictions from the Poisson regression model are correlated with those from the linear model; however, the former are non-negative. As a result the Poisson regression predictions tend to be larger than those from the linear model for either very low or very high levels of ridership.
In this section, we used the glm() function with the argument family = poisson in order to perform Poisson regression. Earlier in this lab we used the glm() function with family = binomial to perform logistic regression. Other choices for the family argument can be used to fit other types of GLMs. For instance, family = Gamma fits a gamma regression model.