GPU-Accelerated Econometrics on Consumer Hardware

tl;dr: A $200 used GPU plugged into an EGPU can make your research code order-of-magnitude faster. Some links to hardware, and test scripts to benchmark your own setup. Consider this a more thorough follow-up to this post on pytorch for econometrics. General principle is most statistics/econometrics comprises of linear-algebra and optimization, which GPUs are great at; use them whenever possible.

GPUs aren’t just for big neural nets models; my torchonometrics package lets you run many workhorse applied econometrics methods on either a CPU or GPU with minimal adjustments required. Many other modern supervised learning methods are also gpu accelerated (eg XGBoost, LightGBM etc.). Jax is also very good for gpu-accelerated statistics [I have a similar library for jaxonometrics ], but I focus on pytorch here since it’s more mature for general ML. Beyond the scope of this writeup, but the GPU is naturally also very useful for local LLMs or fine-tuning small models.

The Hardware Setup

This contraption sits behind my monitor in a (well-ventilated) corner. It is plugged into a framework 13 [12th gen, starting to get a bit creaky], which is quite thin and light and I don’t need to lug around a full gaming PC.

It is comprised of:

• NVIDIA GTX 1070 (8GB, ~$200 used). Popular old (nearly 10 years old!) gaming GPU.
• AOostar AG01 eGPU Dock with included power-supply. These vary widely in form-factor: there are clean black-box ones that will cost you an arm and a leg [dell alienware, obv], or my Rube-goldeberg machine build with a sparse GPU enclosure, power supply, and converter from m.2 to thunderbolt. The AOstar is now one clean package and quite reasonably priced. This is also future-proof and flexible wrt upgrading GPUs later, which is not true of most black-box eGPUs.
• power input for the eGPU dock, and a thunderbolt 3 cable to connect to my laptop.

This gets you GPU compute without needing a desktop or cloud bill. Just plug the eGPU into your laptop via thunderbolt and you’re good. You may also have access to GPUs via university clusters or cloud providers, which you should definitely use, but having one locally is super convenient for development and testing.

GPUs have thousands of tiny cores instead of a CPU’s 4-16 big ones. Matrix math (which is basically all of ML) runs way faster when you can do thousands of multiplications at once.

Here’s a simple linear regression on 1M obs:

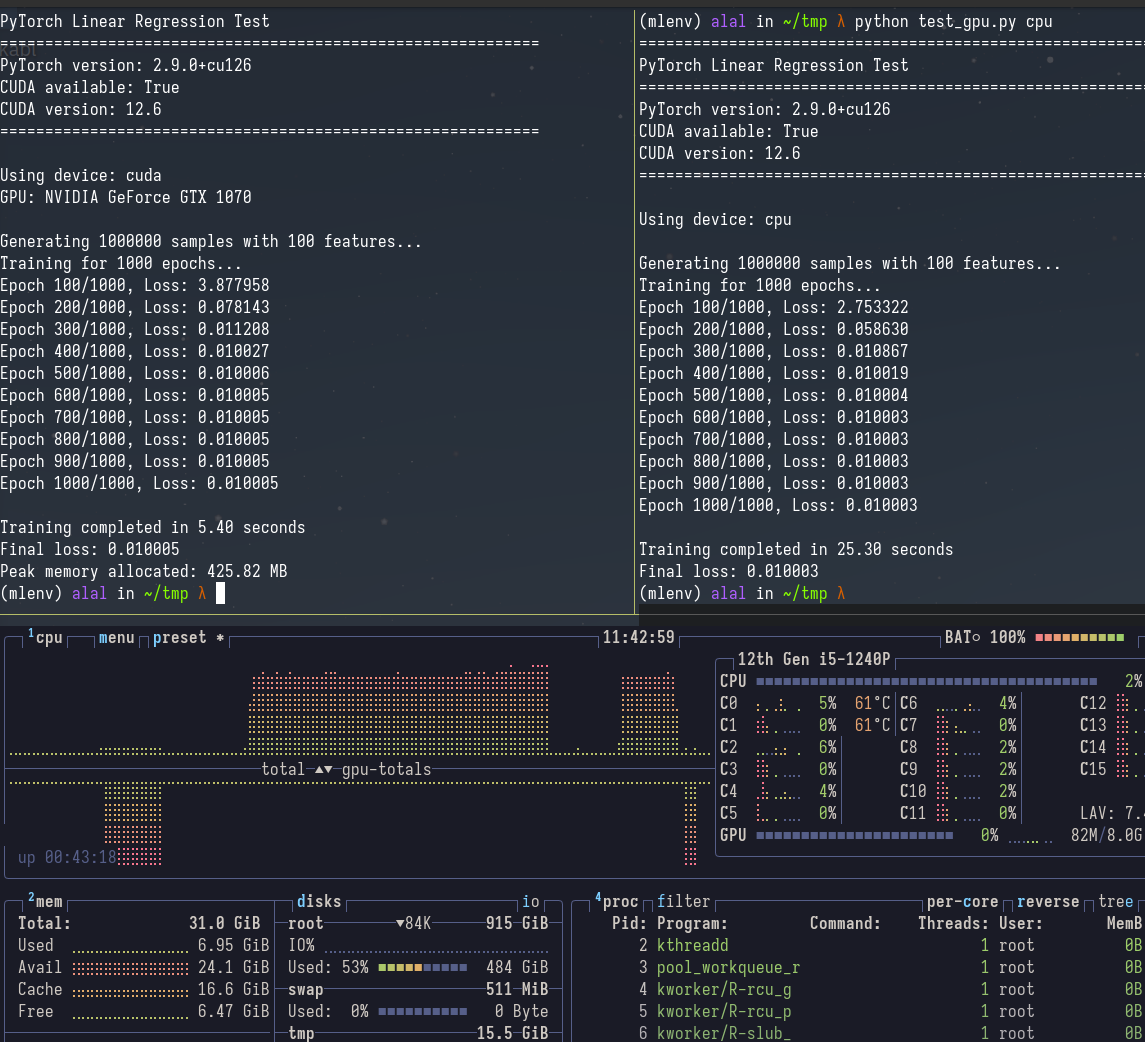
5x speedup on a simple problem. Regression is obv solvable in closed-form, but you might want to do gradient descent to handle large/streaming data, regularization etc. I also have a multinomial logit example below that shows ~10x speedup on a more realistic econometrics problem.

Software Setup

I use ubuntu on my main work machine, but any (not super-obscure) distro should work. Apple silicon users, you’re out of luck - EGPUs aren’t supported for reasons I don’t understand. Don’t do any serious programming on windows to save your sanity.

Setting up is straightforward

# Install NVIDIA drivers
sudo apt install nvidia-driver-535
sudo reboot
nvidia-smi  # verify it worked
 
# Install PyTorch with CUDA
uv venv
source .venv/bin/activate
uv add torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu121
 
# Test it
python -c "import torch; print(torch.cuda.is_available())"  # should print True

Example 1: Linear Regression

The key idea: create tensors on the GPU with device='cuda', then everything stays there. In a real data example, you would use standard python libraries (numpy, polars and the like) and use torch to move them to GPU, or pair it with pytorch’s dataloader to move batches to update gradients (in most realistic settings, that’s the pattern you’d likely want to use).

import sys
import time
 
import torch
 
 
def test_linear_regression(
    device_name="cuda",
    n_samples=1_000_000,
    n_features=100,
    n_epochs=5_000,
    increment=100,
):
    """Simple linear regression test to benchmark CPU vs GPU"""
 
    device = torch.device(device_name)
    print(f"Using device: {device}")
 
    if device.type == "cuda":
        print(f"GPU: {torch.cuda.get_device_name(0)}")
 
    # Generate synthetic data
    print(f"\nGenerating {n_samples} samples with {n_features} features...")
    X = torch.randn(n_samples, n_features, device=device)
    b = torch.randn(n_features, 1, device=device)
    y = X @ b + torch.randn(n_samples, 1, device=device) * 0.1
 
    # Initialize model
    bhat = torch.randn(n_features, 1, device=device, requires_grad=True)
    learning_rate = 0.01
 
    # Training loop
    print(f"Training for {n_epochs} epochs...")
    start_time = time.time()
 
    for epoch in range(n_epochs):
        # Forward pass
        y_pred = X @ bhat
        loss = ((y_pred - y) ** 2).mean()
        # Backward pass
        loss.backward()
        # Update bhat
        with torch.no_grad():
            bhat -= learning_rate * bhat.grad
            bhat.grad.zero_()
        if (epoch + 1) % increment == 0:
            print(f"Epoch {epoch + 1}/{n_epochs}, Loss: {loss.item():.6f}")
 
    end_time = time.time()
    elapsed = end_time - start_time
 
    print(f"\nTraining completed in {elapsed:.2f} seconds")
    print(f"Final loss: {loss.item():.6f}")
 
    if device.type == "cuda":
        print(
            f"Peak memory allocated: {torch.cuda.max_memory_allocated(0) / 1024**2:.2f} MB"
        )
 
    return elapsed
 
 
if __name__ == "__main__":
    device_arg = sys.argv[1] if len(sys.argv) > 1 else "cuda"
 
    print("=" * 60)
    print("PyTorch Linear Regression Test")
    print("=" * 60)
    print(f"PyTorch version: {torch.__version__}")
    print(f"CUDA available: {torch.cuda.is_available()}")
    if torch.cuda.is_available():
        print(f"CUDA version: {torch.version.cuda}")
    print("=" * 60 + "\n")
 
    test_linear_regression(device_arg)

Run python gpu_regression.py cuda vs python gpu_regression.py cpu to see the difference yourself. Here’s the output on my machine

Example 2: Multinomial Logit (Discrete Choice)

A more practical econometrics example - multinomial logit estimation via maximum likelihood. This is the workhorse model for discrete choice analysis (brand choice, transportation mode, location decisions, etc.).

The model estimates choice probabilities using the softmax function:

P(choice=j | x) = exp(x'β_j) / Σ_k exp(x'β_k)

Torchonometrics also has matrix-completion versions of MNL that allow you to fit mixed logit, thereby weakly relaxing the IIA assumption.

We don’t need to write the actual optimization loop anymore since torchonometrics classes subclass off MaximumLikelihoodEstimators that use pytorch optimizers under the hood.

 
import sys
import time
 
import torch
 
from torchonometrics.choice import MultinomialLogit
 
 
def benchmark_mnl(
    device_name="cuda",
    n_samples=10_000_000,
    n_features=20,
    n_choices=10,
):
    """
    Benchmark multinomial logit estimation on CPU vs GPU.
 
    Multinomial logit is the workhorse of discrete choice econometrics.
    Common applications: brand choice, mode choice, location choice.
 
    This estimates choice probabilities via maximum likelihood using softmax:
        P(choice=j | x) = exp(x'β_j) / Σ_k exp(x'β_k)
    """
    device = torch.device(device_name)
    print(f"Using device: {device}")
 
    if device.type == "cuda":
        print(f"GPU: {torch.cuda.get_device_name(0)}")
 
    # Generate synthetic choice data
    print(f"\nGenerating {n_samples} observations with {n_choices} choices...")
    X = torch.randn(n_samples, n_features, device=device)
    X = torch.cat([torch.ones(n_samples, 1, device=device), X], dim=1)  # Add intercept
 
    # True parameters (last choice is base category, normalized to 0)
    true_params = torch.randn(n_features + 1, n_choices - 1, device=device)
    true_params_full = torch.cat(
        [true_params, torch.zeros(n_features + 1, 1, device=device)], dim=1
    )
 
    # Generate choices using softmax probabilities
    logits = X @ true_params_full
    probs = torch.nn.functional.softmax(logits, dim=1)
    choices = torch.multinomial(probs, 1).squeeze(1)
    y_one_hot = torch.nn.functional.one_hot(choices, num_classes=n_choices).to(
        torch.float32
    )
 
    print(
        f"Choice distribution: {torch.bincount(choices, minlength=n_choices).tolist()}"
    )
 
    # Initialize parameters with small random values
    init_params = torch.randn(n_features + 1, n_choices - 1, device=device) * 0.01
 
    # Fit multinomial logit model
    print("\nFitting multinomial logit model...")
    model = MultinomialLogit(maxiter=10_000, tol=1e-6)
 
    start_time = time.time()
    model.fit(X, y_one_hot, init_params=init_params)
    elapsed = time.time() - start_time
 
    print(f"\nEstimation completed in {elapsed:.2f} seconds")
    print(f"Converged in {model.iterations_run} iterations")
 
    # Show parameter recovery
    estimated_params = model.params["coef"]
    estimated_params_full = torch.cat(
        [estimated_params, torch.zeros(n_features + 1, 1, device=device)], dim=1
    )
 
    # Compare first few coefficients
    print("\nParameter recovery (first 3 features, first 2 choices):")
    print(f"True params:\n{true_params_full[:3, :2]}")
    print(f"Estimated params:\n{estimated_params_full[:3, :2]}")
 
    # Prediction accuracy
    y_pred_probs = model.predict_proba(X)
    y_pred = torch.argmax(y_pred_probs, dim=1)
    accuracy = (y_pred == choices).float().mean()
    print(f"\nIn-sample prediction accuracy: {accuracy:.2%}")
 
    if device.type == "cuda":
        print(
            f"Peak memory allocated: {torch.cuda.max_memory_allocated(0) / 1024**2:.2f} MB"
        )
 
    return elapsed
 
 
if __name__ == "__main__":
    device_arg = sys.argv[1] if len(sys.argv) > 1 else "cuda"
 
    print("=" * 60)
    print("Multinomial Logit Estimation Benchmark")
    print("=" * 60)
    print(f"PyTorch version: {torch.__version__}")
    print(f"CUDA available: {torch.cuda.is_available()}")
    if torch.cuda.is_available():
        print(f"CUDA version: {torch.version.cuda}")
    print("=" * 60 + "\n")
 
    benchmark_mnl(device_arg)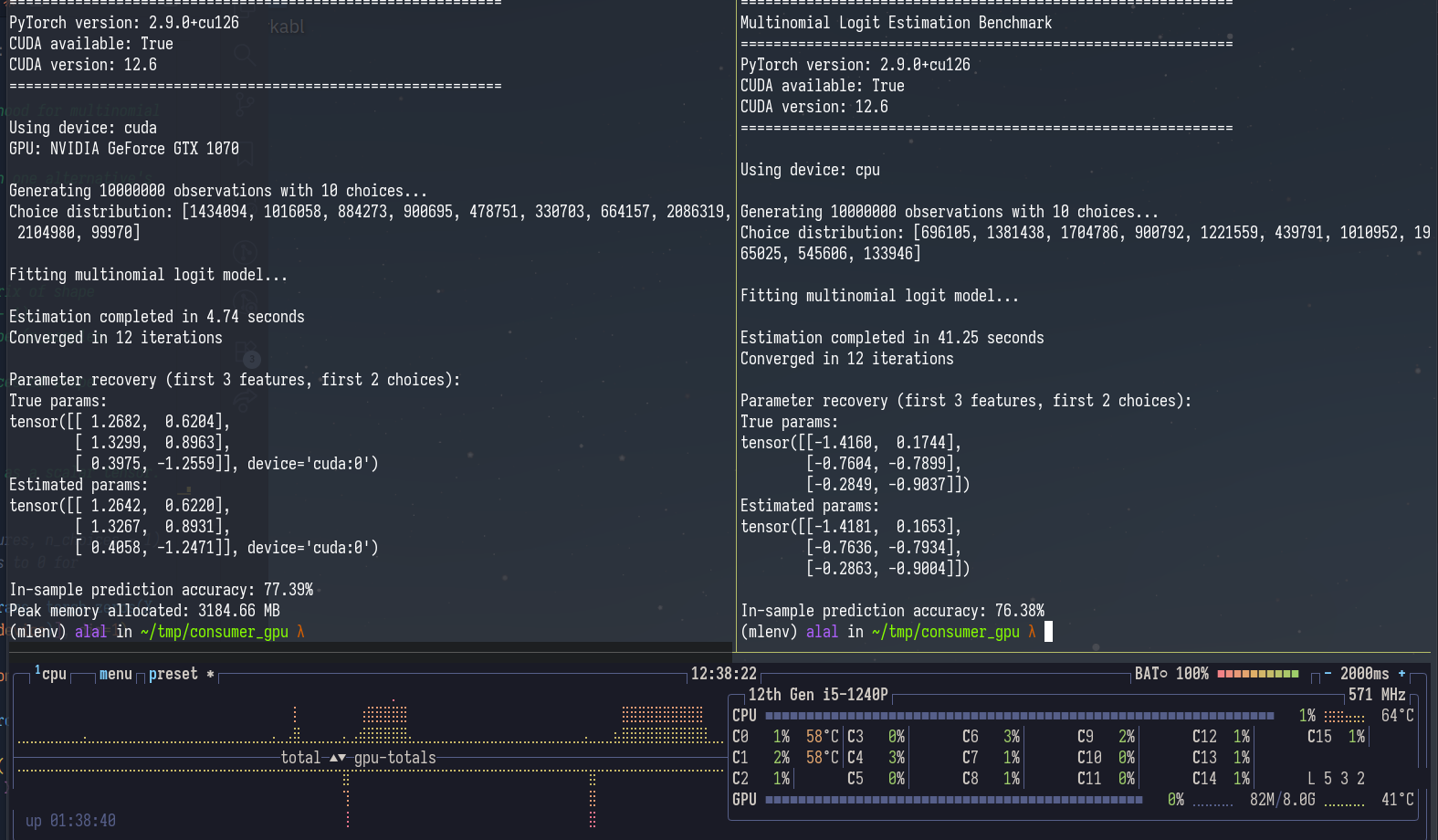

~10x speedup for MNL estimation on 10m obs with 10 alternatives.

The Pattern

Converting CPU code to GPU code is usually just:

1. Pick a device:

   device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

2. Create tensors on that device:

   X = torch.randn(1000, 100, device=device)  # new tensor
   X = X.to(device)  # existing tensor

3. Move models to device:

   model = MyModel().to(device)

That’s it. PyTorch handles the rest. Adapt the pattern to your own code. Start by just adding device = torch.device("cuda") and .to(device) calls. See if it’s faster. If not, profile to see where time is spent.

When GPU Helps

Good:

• Big datasets (>100k samples)
• Matrix-heavy ops (anything with @ or .matmul())
• Deep models (many layers)
• Iterative algorithms (EM, gradient descent, MCMC)

Bad:

• Tiny datasets (<10k samples)
• Lots of CPU-GPU data movement
• I/O bound code (loading files, preprocessing)
• Simple operations on small tensors

Rule of thumb: if your CPU fan spins up, try GPU. If your code spends most time loading data or in pandas/polars, GPU won’t help. Anything that involves big matrix math will likely speed up when you move to GPU.

Resources

• PyTorch docs
• CUDA installation guide
• PyTorch performance tuning