Numpy Basics

In [1]:
import numpy as np

x = np.random.uniform(0, 1, size=1000000)
x.mean()
Out[1]:
0.5005185737403215

Basic Objects

In [2]:
a = np.zeros(3)
a
Out[2]:
array([0., 0., 0.])
In [3]:
type(a)
Out[3]:
numpy.ndarray
In [4]:
a = np.zeros(3)
type(a[0])
Out[4]:
numpy.float64
In [5]:
a = np.zeros(3, dtype=int)
type(a[0])
Out[5]:
numpy.int64
In [6]:
z = np.zeros(10)
In [7]:
z.shape
Out[7]:
(10,)
In [8]:
z.shape = (10, 1)
z
Out[8]:
array([[0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.]])
In [9]:
z = np.zeros(4)
z.shape = (2, 2)
z
Out[9]:
array([[0., 0.],
       [0., 0.]])
In [10]:
z = np.empty(3)
z
Out[10]:
array([0., 0., 0.])
In [97]:
z = np.linspace(2, 4, 5)  # From 2 to 4, with 5 elements
z
Out[97]:
array([2. , 2.5, 3. , 3.5, 4. ])
In [12]:
z = np.identity(2)
z
Out[12]:
array([[1., 0.],
       [0., 1.]])
In [13]:
z = np.array([10, 20])                 # ndarray from Python list
z
Out[13]:
array([10, 20])
In [14]:
type(z)
Out[14]:
numpy.ndarray
In [15]:
z = np.array((10, 20), dtype=float)    # Here 'float' is equivalent to 'np.float64'
z
Out[15]:
array([10., 20.])
In [16]:
z = np.array([[1, 2], [3, 4]])         # 2D array from a list of lists
z
Out[16]:
array([[1, 2],
       [3, 4]])
In [17]:
na = np.linspace(10, 20, 2)
na is np.asarray(na)   # Does not copy NumPy arrays
Out[17]:
True
In [18]:
na is np.array(na)     # Does make a new copy --- perhaps unnecessarily
Out[18]:
False

Indexing

In [19]:
z = np.linspace(1, 2, 5)

z
Out[19]:
array([1.  , 1.25, 1.5 , 1.75, 2.  ])
In [20]:
z[0]
Out[20]:
1.0
In [21]:
z[0:2]  # Two elements, starting at element 0
Out[21]:
array([1.  , 1.25])
In [22]:
z[-1]
Out[22]:
2.0
In [23]:
z = np.array([[1, 2], [3, 4]])
z
Out[23]:
array([[1, 2],
       [3, 4]])
In [24]:
z[0, 0]
Out[24]:
1
In [25]:
z[0, 1]
Out[25]:
2
In [26]:
z[0,:]
Out[26]:
array([1, 2])
In [27]:
z[:,1]
Out[27]:
array([2, 4])
In [28]:
z = np.linspace(2, 4, 5)
z
Out[28]:
array([2. , 2.5, 3. , 3.5, 4. ])
In [29]:
indices = np.array((0, 2, 3))
z[indices]
Out[29]:
array([2. , 3. , 3.5])
In [30]:
z
Out[30]:
array([2. , 2.5, 3. , 3.5, 4. ])
In [31]:
d = np.array([0, 1, 1, 0, 0], dtype=bool)
d
Out[31]:
array([False,  True,  True, False, False])
In [32]:
z[d]
Out[32]:
array([2.5, 3. ])
In [33]:
z = np.empty(3)
z
Out[33]:
array([2. , 3. , 3.5])
In [34]:
z[:] = 42
z
Out[34]:
array([42., 42., 42.])
In [35]:
a = np.array((4, 3, 2, 1))
a
Out[35]:
array([4, 3, 2, 1])

Mathematical Operations

In [36]:
a.sort()              # Sorts a in place
a
Out[36]:
array([1, 2, 3, 4])
In [37]:
a.sum()               # Sum
Out[37]:
10
In [38]:
a.mean()              # Mean
Out[38]:
2.5
In [39]:
a.max()               # Max
Out[39]:
4
In [40]:
a.argmax()            # Returns the index of the maximal element
Out[40]:
3
In [41]:
a.cumsum()            # Cumulative sum of the elements of a
Out[41]:
array([ 1,  3,  6, 10])
In [42]:
a.cumprod()           # Cumulative product of the elements of a
Out[42]:
array([ 1,  2,  6, 24])
In [43]:
a.var()               # Variance
Out[43]:
1.25
In [44]:
a.std()               # Standard deviation
Out[44]:
1.118033988749895
In [45]:
a.shape = (2, 2)
a.T                   # Equivalent to a.transpose()
Out[45]:
array([[1, 3],
       [2, 4]])
In [46]:
z = np.linspace(2, 4, 5)
z
Out[46]:
array([2. , 2.5, 3. , 3.5, 4. ])
In [47]:
z.searchsorted(2.2)
Out[47]:
1
In [48]:
a = np.array((4, 3, 2, 1))
In [49]:
np.sum(a)
Out[49]:
10
In [50]:
np.mean(a)
Out[50]:
2.5
In [51]:
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
a + b
Out[51]:
array([ 6,  8, 10, 12])
In [52]:
a * b
Out[52]:
array([ 5, 12, 21, 32])
In [53]:
a + 10
Out[53]:
array([11, 12, 13, 14])
In [54]:
a * 10
Out[54]:
array([10, 20, 30, 40])
In [55]:
A = np.ones((2, 2))
B = np.ones((2, 2))
A + B
Out[55]:
array([[2., 2.],
       [2., 2.]])
In [56]:
A + 10
Out[56]:
array([[11., 11.],
       [11., 11.]])
In [57]:
A * B
Out[57]:
array([[1., 1.],
       [1., 1.]])
In [58]:
import numpy as np

A = np.ones((2, 2))
B = np.ones((2, 2))
A @ B
Out[58]:
array([[2., 2.],
       [2., 2.]])
In [59]:
A = np.array((1, 2))
B = np.array((10, 20))
A @ B
Out[59]:
50
In [60]:
A = np.array(((1, 2), (3, 4)))
A
Out[60]:
array([[1, 2],
       [3, 4]])
In [61]:
A @ (0, 1)
Out[61]:
array([2, 4])
In [62]:
a = np.array([42, 44])
a
Out[62]:
array([42, 44])
In [63]:
a[-1] = 0  # Change last element to 0
a
Out[63]:
array([42,  0])
In [64]:
a = np.random.randn(3)
a
Out[64]:
array([ 1.19628863,  0.26587826, -0.79166651])
In [65]:
b = a
b[0] = 0.0
a
Out[65]:
array([ 0.        ,  0.26587826, -0.79166651])
In [66]:
a = np.random.randn(3)
a
Out[66]:
array([-0.30505792,  0.07557764, -0.86360824])
In [67]:
b = np.empty_like(a)
np.copyto(b, a)        # to b, from a
b
Out[67]:
array([-0.30505792,  0.07557764, -0.86360824])
In [68]:
b[:] = 1
b
Out[68]:
array([1., 1., 1.])
In [69]:
a
Out[69]:
array([-0.30505792,  0.07557764, -0.86360824])
In [70]:
z = np.array([1, 2, 3])
np.sin(z)
Out[70]:
array([0.84147098, 0.90929743, 0.14112001])
In [71]:
n = len(z)
y = np.empty(n)
for i in range(n):
    y[i] = np.sin(z[i])
In [72]:
z
Out[72]:
array([1, 2, 3])
In [73]:
(1 / np.sqrt(2 * np.pi)) * np.exp(- 0.5 * z**2)
Out[73]:
array([0.24197072, 0.05399097, 0.00443185])
In [74]:
def f(x):
    return 1 if x > 0 else 0
In [75]:
import numpy as np

x = np.random.randn(4)
x
Out[75]:
array([-0.80604611,  1.95930447, -1.04051728, -0.37767133])
In [76]:
np.where(x > 0, 1, 0)  # Insert 1 if x > 0 true, otherwise 0
Out[76]:
array([0, 1, 0, 0])
In [77]:
def f(x): return 1 if x > 0 else 0

f = np.vectorize(f)
f(x)                # Passing the same vector x as in the previous example
Out[77]:
array([0, 1, 0, 0])
In [78]:
z = np.array([2, 3])
y = np.array([2, 3])
z == y
Out[78]:
array([ True,  True])
In [79]:
y[0] = 5
z == y
Out[79]:
array([False,  True])
In [80]:
z != y
Out[80]:
array([ True, False])
In [81]:
z = np.linspace(0, 10, 5)
z
Out[81]:
array([ 0. ,  2.5,  5. ,  7.5, 10. ])
In [82]:
z > 3
Out[82]:
array([False, False,  True,  True,  True])
In [83]:
b = z > 3
b
Out[83]:
array([False, False,  True,  True,  True])
In [84]:
z[b]
Out[84]:
array([ 5. ,  7.5, 10. ])
In [85]:
z[z > 3]
Out[85]:
array([ 5. ,  7.5, 10. ])
In [86]:
z = np.random.randn(10000)  # Generate standard normals
y = np.random.binomial(10, 0.5, size=1000)    # 1,000 draws from Bin(10, 0.5)
y.mean()
Out[86]:
5.025
In [87]:
A = np.array([[1, 2], [3, 4]])

np.linalg.det(A)           # Compute the determinant
Out[87]:
-2.0000000000000004
In [88]:
np.linalg.inv(A)           # Compute the inverse
Out[88]:
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
In [89]:
from random import uniform

def sample(q):
    a = 0.0
    U = uniform(0, 1)
    for i in range(len(q)):
        if a < U <= a + q[i]:
            return i
        a = a + q[i]
In [90]:
import numpy as np
import matplotlib.pyplot as plt
In [91]:
def p(x, coef):
    X = np.empty(len(coef))
    X[0] = 1
    X[1:] = x
    y = np.cumprod(X)   # y = [1, x, x**2,...]
    return coef @ y
In [92]:
coef = np.ones(3)
print(coef)
print(p(1, coef))
# For comparison
q = np.poly1d(coef)
print(q(1))

[1. 1. 1.]
3.0
3.0
In [93]:
from numpy import cumsum
from numpy.random import uniform

class discreteRV:
    """
    Generates an array of draws from a discrete random variable with vector of
    probabilities given by q.
    """

    def __init__(self, q):
        """
        The argument q is a NumPy array, or array like, nonnegative and sums
        to 1
        """
        self.q = q
        self.Q = cumsum(q)

    def draw(self, k=1):
        """
        Returns k draws from q. For each such draw, the value i is returned
        with probability q[i].
        """
        return self.Q.searchsorted(uniform(0, 1, size=k))
In [94]:
q = (0.1, 0.9)
d = discreteRV(q)
d.q = (0.5, 0.5)
In [95]:
"""
Modifies ecdf.py from QuantEcon to add in a plot method

"""

class ECDF:
    """
    One-dimensional empirical distribution function given a vector of
    observations.

    Parameters
    ----------
    observations : array_like
        An array of observations

    Attributes
    ----------
    observations : array_like
        An array of observations

    """

    def __init__(self, observations):
        self.observations = np.asarray(observations)

    def __call__(self, x):
        """
        Evaluates the ecdf at x

        Parameters
        ----------
        x : scalar(float)
            The x at which the ecdf is evaluated

        Returns
        -------
        scalar(float)
            Fraction of the sample less than x

        """
        return np.mean(self.observations <= x)

    def plot(self, a=None, b=None):
        """
        Plot the ecdf on the interval [a, b].

        Parameters
        ----------
        a : scalar(float), optional(default=None)
            Lower end point of the plot interval
        b : scalar(float), optional(default=None)
            Upper end point of the plot interval

        """

        # === choose reasonable interval if [a, b] not specified === #
        if a is None:
            a = self.observations.min() - self.observations.std()
        if b is None:
            b = self.observations.max() + self.observations.std()

        # === generate plot === #
        x_vals = np.linspace(a, b, num=100)
        f = np.vectorize(self.__call__)
        plt.plot(x_vals, f(x_vals))
        plt.show()
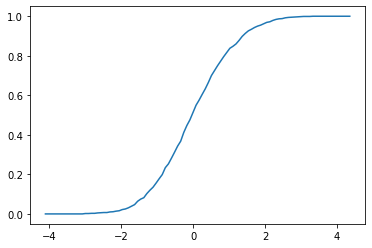
In [96]:
X = np.random.randn(1000)
F = ECDF(X)
F.plot()