Introduction to Spatial Data Analysis in Python¶
In [1]:
import os, sys, glob
from pathlib import Path
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# vector / visualisation packages
import geopandas as gpd
import geoplot as gplt
import mapclassify as mc
import geoplot.crs as gcrs
from earthpy import clip as cl
# raster packages
import rasterio as rio
import georasters as gr
from rasterstats import zonal_stats
# spatial econometrics
import pysal as ps
import esda
import libpysal as lps
from pysal.lib.weights.weights import W
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
Vector data¶
From Natural Earth
In [2]:
cities = gpd.read_file("https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/110m/cultural/ne_110m_populated_places.zip")
In [3]:
countries = gpd.read_file('https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/10m/cultural/ne_10m_admin_0_countries.zip')
In [4]:
countries.head()
Out[4]:
In [5]:
cities.head()
Out[5]:
Constructing Geodataframe from lon-lat¶
In [6]:
df = pd.DataFrame({'City': ['Buenos Aires', 'Brasilia', 'Santiago', 'Bogota', 'Caracas'],
'Country': ['Argentina', 'Brazil', 'Chile', 'Colombia', 'Venezuela'],
'Latitude': [-34.58, -15.78, -33.45, 4.60, 10.48],
'Longitude': [-58.66, -47.91, -70.66, -74.08, -66.86]})
lat_am_capitals = gpd.GeoDataFrame(df, geometry = gpd.points_from_xy(df.Longitude, df.Latitude))
Making Maps¶
In [7]:
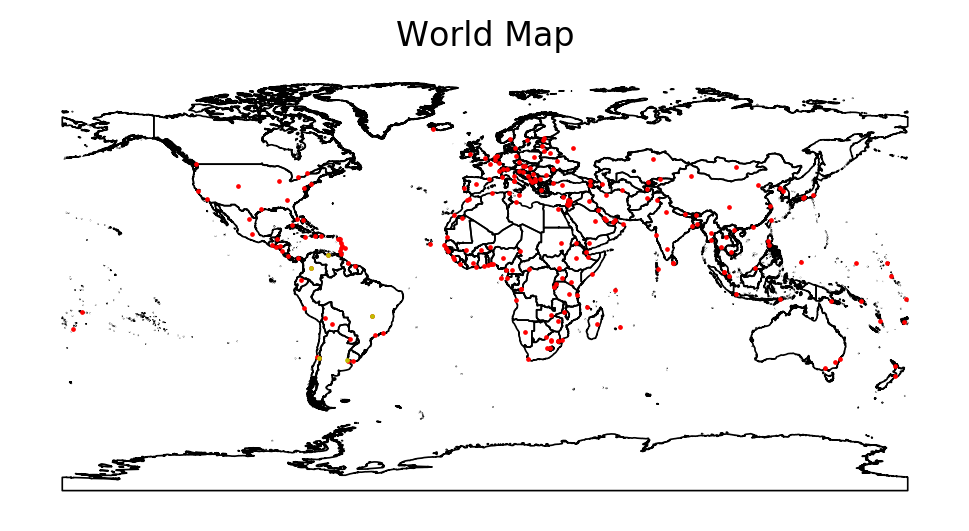
f, ax = plt.subplots(dpi = 200)
countries.plot(edgecolor = 'k', facecolor = 'None', linewidth = 0.6, ax = ax)
cities.plot(markersize = 0.5, facecolor = 'red', ax = ax)
lat_am_capitals.plot(markersize = 0.5, facecolor = 'y', ax = ax)
ax.set_title('World Map')
ax.set_axis_off()
Out[7]:
Out[7]:
Out[7]:
Out[7]:
Static Webmaps¶
In [8]:
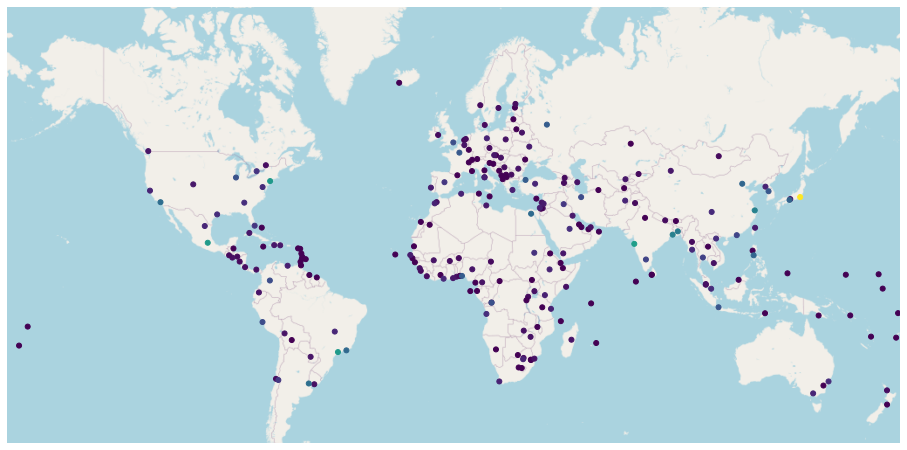
ax = gplt.webmap(countries, projection=gplt.crs.WebMercator(), figsize = (16, 12))
gplt.pointplot(cities, ax=ax, hue = 'POP2015')
Out[8]:
Aside on Projections¶
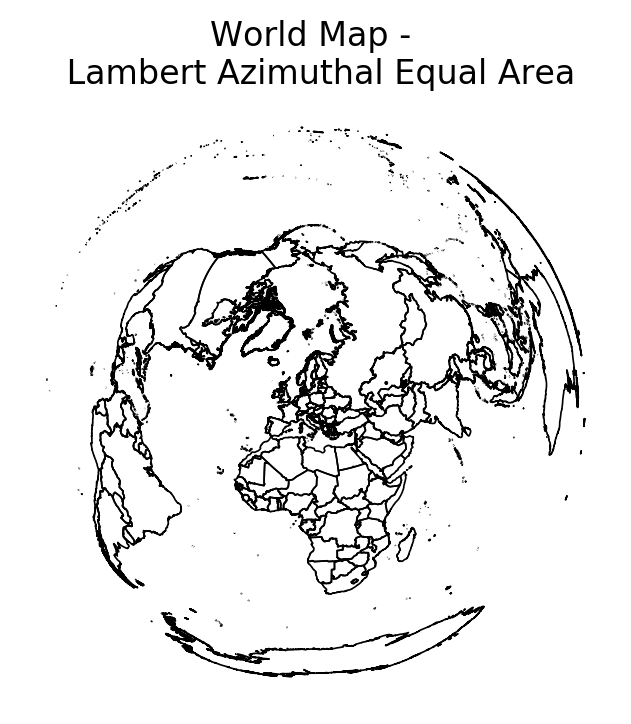
Map projections flatten a globe's surface onto a 2D plane. This necessarily distorts the surface (one of Gauss' lesser known results), so one must choose specific form of 'acceptable' distortion.
By convention, the standard projection in GIS is World Geodesic System(lat/lon - WGS84). This is a cylindrical projection, which stretches distances east-west and results in incorrect distance and areal calculations. For accurate distance and area calculations, try to use UTM (which divides map into zones). See epsg.io
In [9]:
countries.crs
Out[9]:
In [10]:
countries_2 = countries.copy()
countries_2 = countries_2.to_crs({'init': 'epsg:3035'})
In [11]:
f, ax = plt.subplots(dpi = 200)
countries_2.plot(edgecolor = 'k', facecolor = 'None', linewidth = 0.6, ax = ax)
ax.set_title('World Map - \n Lambert Azimuthal Equal Area')
ax.set_axis_off()
Out[11]:
Out[11]:
Choropleths¶
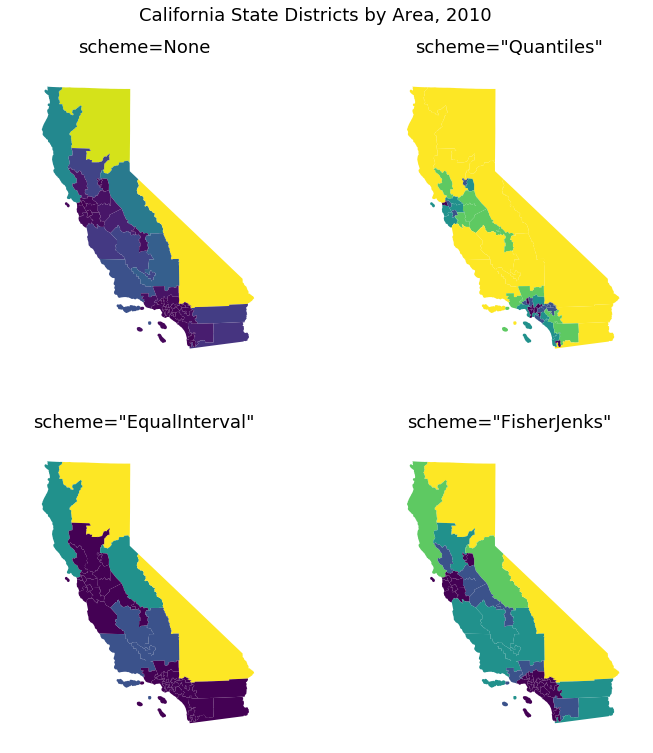
Maps with color-coding based on value in table
- scheme=None—A continuous colormap.
- scheme=”Quantiles”—Bins the data such that the bins contain equal numbers of samples.
- scheme=”EqualInterval”—Bins the data such that bins are of equal length.
- scheme=”FisherJenks”—Bins the data using the Fisher natural breaks optimization procedure.
(Example from geoplots gallery)
In [12]:
cali = gpd.read_file(gplt.datasets.get_path('california_congressional_districts'))
cali['area'] =cali.geometry.area
proj=gcrs.AlbersEqualArea(central_latitude=37.16611, central_longitude=-119.44944)
fig, axarr = plt.subplots(2, 2, figsize=(12, 12), subplot_kw={'projection': proj})
gplt.choropleth(
cali, hue='area', linewidth=0, scheme=None, ax=axarr[0][0]
)
axarr[0][0].set_title('scheme=None', fontsize=18)
scheme = mc.Quantiles(cali.area, k=5)
gplt.choropleth(
cali, hue='area', linewidth=0, scheme=scheme, ax=axarr[0][1]
)
axarr[0][1].set_title('scheme="Quantiles"', fontsize=18)
scheme = mc.EqualInterval(cali.area, k=5)
gplt.choropleth(
cali, hue='area', linewidth=0, scheme=scheme, ax=axarr[1][0]
)
axarr[1][0].set_title('scheme="EqualInterval"', fontsize=18)
scheme = mc.FisherJenks(cali.area, k=5)
gplt.choropleth(
cali, hue='area', linewidth=0, scheme=scheme, ax=axarr[1][1]
)
axarr[1][1].set_title('scheme="FisherJenks"', fontsize=18)
plt.subplots_adjust(top=0.92)
plt.suptitle('California State Districts by Area, 2010', fontsize=18)
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Out[12]:
Spatial Merge¶
Subset to Africa
In [13]:
afr = countries.loc[countries.CONTINENT == 'Africa']
afr.plot()
Out[13]:
Subset cities by merging with African boundaries
In [14]:
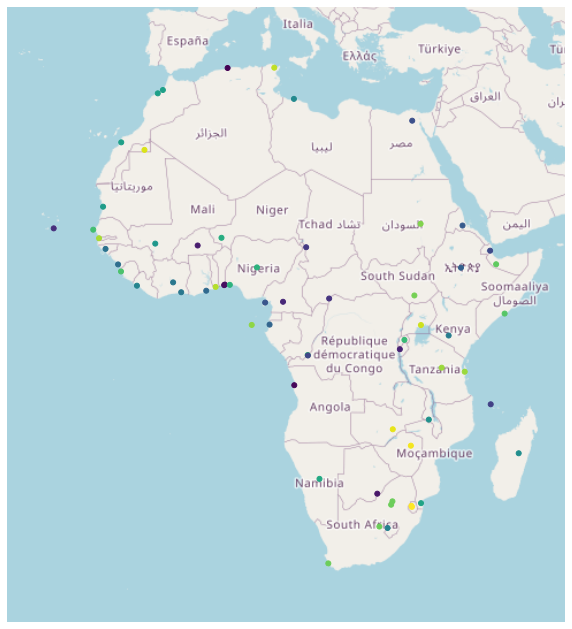
afr_cities = gpd.sjoin(cities, afr, how='inner')
In [15]:
ax = gplt.webmap(afr, projection=gplt.crs.WebMercator(), figsize = (10, 14))
gplt.pointplot(afr_cities, ax=ax, hue = 'NAME_EN')
Out[15]:
In [16]:
afr_cities.head()
Out[16]:
Distance Calculations¶
In [17]:
rivers = gpd.read_file('https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/50m/physical/ne_50m_rivers_lake_centerlines.zip')
In [18]:
rivers.geometry.head()
Out[18]:
In [19]:
rivers.plot()
Out[19]:
In [20]:
def min_distance(point, lines = rivers):
return lines.distance(point).min()
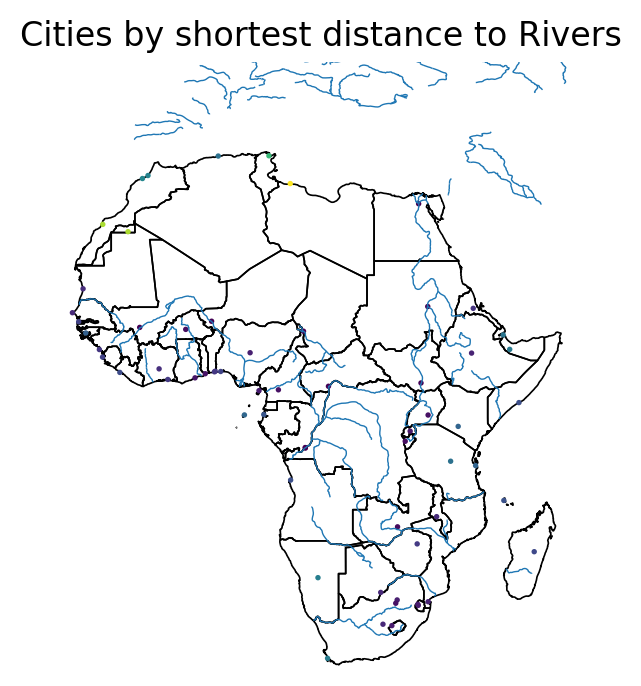
afr_cities['min_dist_to_rivers'] = afr_cities.geometry.apply(min_distance)
In [21]:
f, ax = plt.subplots(dpi = 200)
afr.plot(edgecolor = 'k', facecolor = 'None', linewidth = 0.6, ax = ax)
rivers.plot(ax = ax, linewidth = 0.5)
afr_cities.plot(column = 'min_dist_to_rivers', markersize = 0.9, ax = ax)
ax.set_ylim(-35, 50)
ax.set_xlim(-20, 55)
ax.set_title('Cities by shortest distance to Rivers')
ax.set_axis_off()
Out[21]:
Out[21]:
Out[21]:
Out[21]:
Out[21]:
Out[21]:
Buffers¶
In [22]:
afr_cities_buf = afr_cities.buffer(1)
In [23]:
f, ax = plt.subplots(dpi = 200)
afr.plot(facecolor = 'None', edgecolor = 'k', linewidth = 0.1, ax = ax)
afr_cities_buf.plot(ax=ax, linewidth=0)
afr_cities.plot(ax=ax, markersize=.2, color='yellow')
ax.set_title('1 decimal degree buffer \n Major cities in Africa', fontsize = 12)
ax.set_axis_off()
Out[23]:
Out[23]:
Out[23]:
Out[23]:
Raster Data¶
In [24]:
raster = 'data/res03_crav6190h_sihr_cer.tif'
In [25]:
# Get info on raster
NDV, xsize, ysize, GeoT, Projection, DataType = gr.get_geo_info(raster)
grow = gr.load_tiff(raster)
grow = gr.GeoRaster(grow, GeoT, projection = Projection)
In [26]:
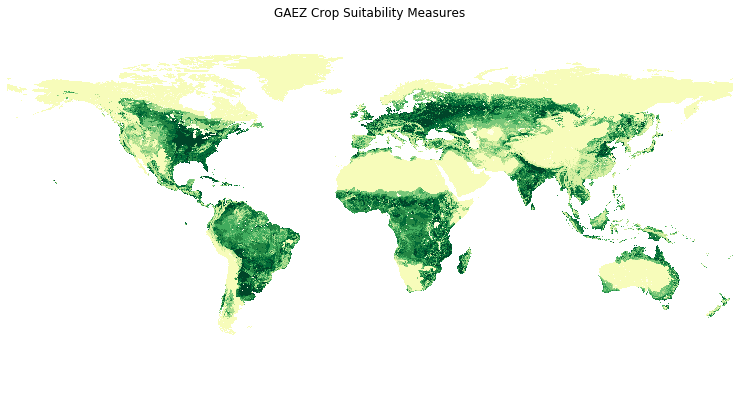
f, ax = plt.subplots(1, figsize=(13, 11))
grow.plot(ax = ax, cmap = 'YlGn_r')
ax.set_title('GAEZ Crop Suitability Measures')
ax.set_axis_off()
Out[26]:
Out[26]:
Clipping Raster¶
In [27]:
brazil = countries.query('ADMIN == "Brazil"')
In [28]:
grow_clip = grow.clip(brazil)[0]
In [29]:
f, ax = plt.subplots(1, figsize=(13, 11))
grow_clip.plot(ax = ax, cmap = 'YlGn_r')
ax.set_title('GAEZ Crop Suitability Measures')
ax.set_axis_off()
Out[29]:
Out[29]:
Zonal Statistics¶
In [30]:
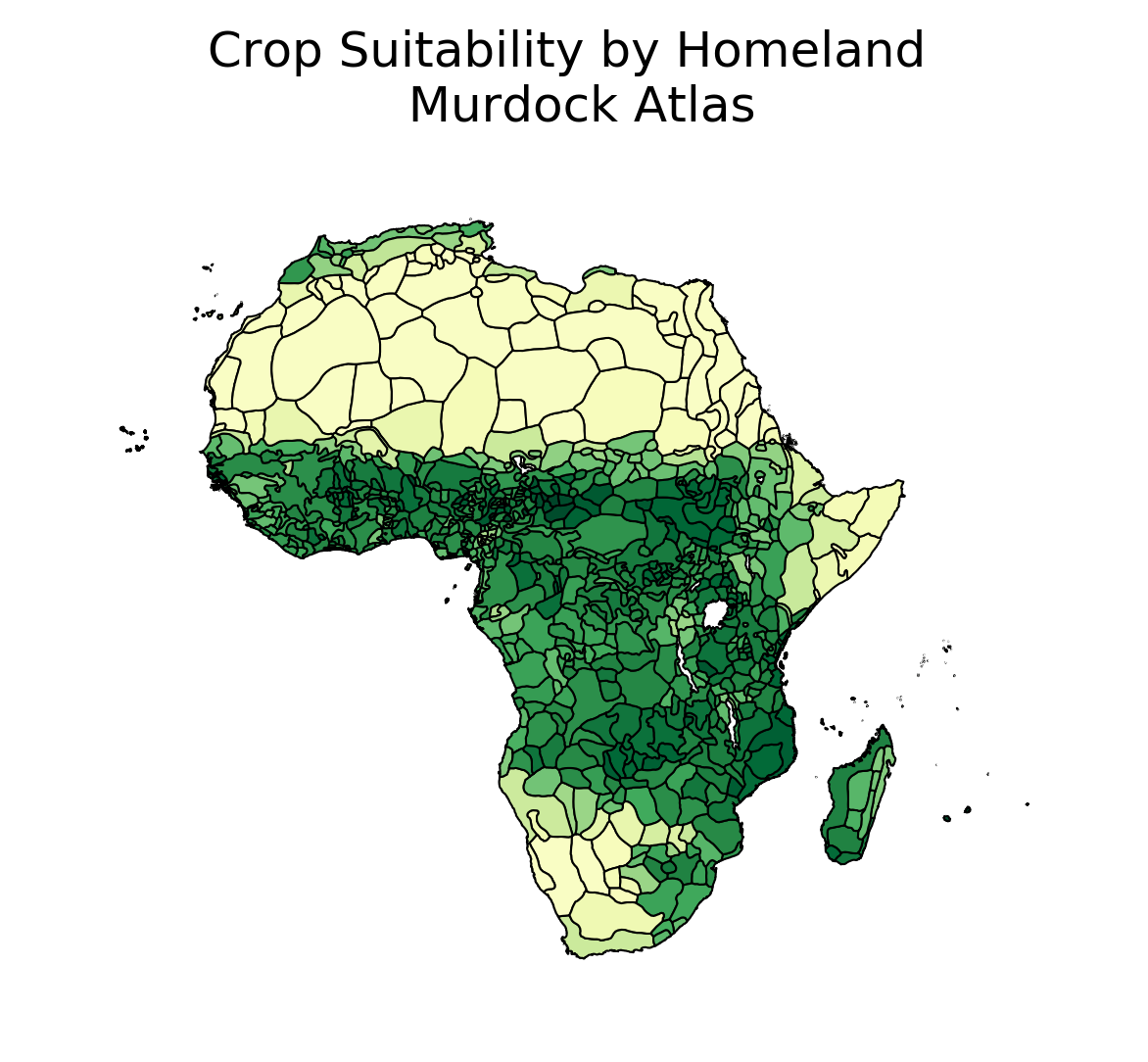
murdock = gpd.read_file('https://scholar.harvard.edu/files/nunn/files/murdock_shapefile.zip')
In [31]:
murdock_cs = gpd.GeoDataFrame.from_features((zonal_stats(murdock, raster, geojson_out = True)))
In [32]:
f, ax = plt.subplots(dpi = 300)
gplt.choropleth(
murdock_cs, hue='mean', linewidth=.5, cmap='YlGn_r', ax=ax
)
ax.set_title('Crop Suitability by Homeland \n Murdock Atlas', fontsize = 12)
Out[32]:
Out[32]:
Spatial Econometrics¶
Weight Matrices¶
In [33]:
%time w = lps.weights.Queen.from_dataframe(murdock_cs)
In [34]:
w.n
w.mean_neighbors
Out[34]:
Out[34]:
In [35]:
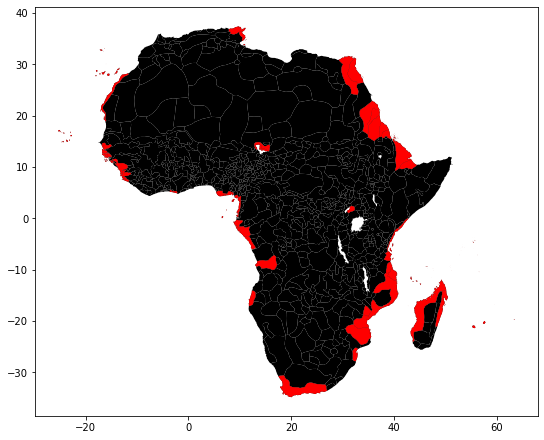
ax = murdock_cs.plot(color='k', figsize=(9, 9))
murdock_cs.loc[w.islands, :].plot(color='red', ax=ax);
In [36]:
mur = murdock_cs.drop(w.islands)
In [37]:
%time w = lps.weights.Queen.from_dataframe(mur)
w.transform = 'r'
Moran's I¶
Measure of spatial correlation
$$I = \frac{N}{W} \frac{\sum_i \sum_j w_{ij} (x_i - \bar{x} ) ( x_j - \bar{x} ) }{ \sum_i (x_i - \bar{x})^2 }$$where $N$ is the total number of units, $x$ is the variable of interest, $w_{ij}$ is the spatial weight between units $i$ and $j$, and $W$ is the sum of all weights $w_{ij}$
$I \in [-1, 1]$. Under null of no spatial correlation, $E(I) = \frac{-1}{N-1} \rightarrow 0$ with large $N$.
In [38]:
mur.shape
Out[38]:
In [39]:
mi = esda.moran.Moran(mur['mean'], w)
mi.I
mi.p_sim
Out[39]:
Out[39]:
Spatial Lag¶
In [40]:
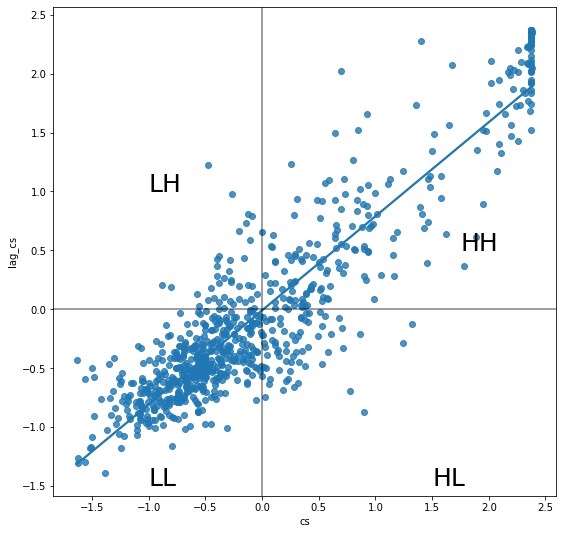
mur['cs'] = (mur['mean'] - mur['mean'].mean()) / mur['mean'].std()
In [41]:
mur['lag_cs'] = lps.weights.lag_spatial(w, mur['cs'])
In [42]:
f, ax = plt.subplots(1, figsize=(9, 9))
# Plot values
sns.regplot(x='cs', y='lag_cs', data=mur, ci=None)
# Add vertical and horizontal lines
plt.axvline(0, c='k', alpha=0.5)
plt.axhline(0, c='k', alpha=0.5)
plt.text(1.75, 0.5, "HH", fontsize=25)
plt.text(1.5, -1.5, "HL", fontsize=25)
plt.text(-1, 1, "LH", fontsize=25)
plt.text(-1.0, -1.5, "LL", fontsize=25)
# Display
plt.show()
Out[42]:
Out[42]:
Out[42]:
Out[42]:
Out[42]:
Out[42]:
Out[42]:
More¶
- Local Indicators of Spatial Autocorrelation (spatial clustering)
- Conley SEs
- Gaussian Random Fields