self-promotion
-
Lal and Woodward is a work-in-progress poster on a decision-theoretic motivation for tiebreaker designs, which are a hybrid of RCTs and RDDs. We propose a notion of ‘lifecycle utility/regret’ that sums over in-experiment payoffs (which are frequently large and tend to be ignored in traditional experimentation) and post-experiment payoffs, and find interior solutions (i.e. tiebreakers that deviate from pure RCTs or RDDs) in a wide variety of parameter values. See Kyle’s exposition here. My general pitch for this line of work is that large swathes of the economy don’t use experimentation because the opportunity costs of experimentation are perceived to be too high [and heterogeneous: decision makers frequently say things like ‘we know this works and putting our biggest customer in the control group is leaving money on the table’] - this framework takes these opportunity costs seriously and provides a formalism to think about them in a way that still allows for credible causal inference but also respects the business’ need to not leave money on the table during experimentation.
-
long and squiggly panel data - short post validating parallel trends using ideas from permutation testing.
-
torchonometrics has come quite a way since I last mentioned it; it now has a full suite of choice models (with a dynamic choice model PR close to being merged), and also automagically handles CPU/GPU switching.
- this set of scripts - largely vibecoded - shows enormous gains from pushing routine econometric estimation tasks to the GPU. Blackwell GPUs are incredibly fast.
-
duckreg now supports compressed PLM / DML - I found a neat leave-out estimation trick for the celebrated partially linear model of Robinson (now rebranded as DML) using leave-out linear smoothers with no tuning parameters from a short ecta paper in the 1990s. This admits to a fully compressed implementation where the discrete covariate is a cartesian product of all categorical variables, and avoids all kinds of expensive cross-fitting and hyperparameter tuning required from traditional supervised learning methods for nuisance functions. Potentially large speedups for applied researchers doing DML with high-cardinality discrete covariates (which is quite frequent in my experience).
-
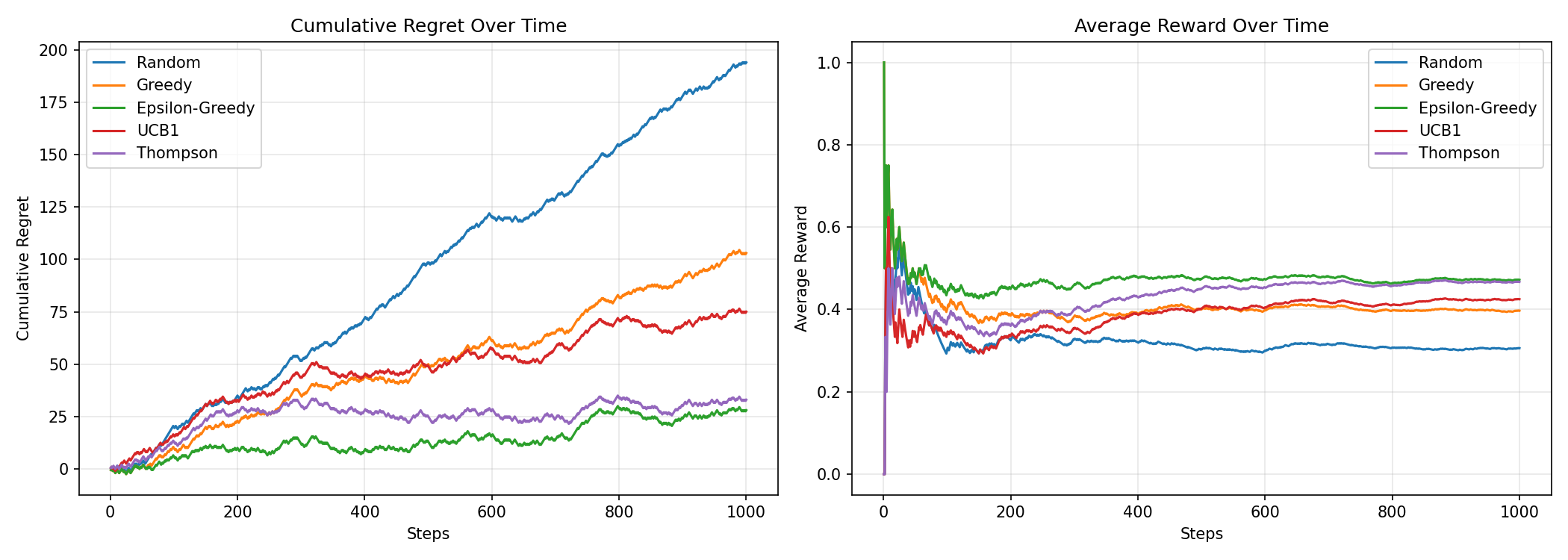
rovingbandit is a small library for various adaptive experimentation methods that I wrote because I couldn’t find a clean set of implementations for what I’m looking for in a single place [full blown RL environments are too much of a headache, especially so in the LLM age where they’re used for quite bespoke applications far removed from statistics]. The basic idea is to support different objectives (best arm id, regret minimization, variance minimization) X (bandit algorithms) X (online / batched updates) in a modular fashion. The main idea is to modularize things so that the environment, objective, algorithm, and runner are all separate components that can be mixed and matched. Here’s a small example script that compares various bandit algorithms on a simple 5-arm Bernoulli bandit problem.
import numpy as np
from rovingbandit import (
# environment
BanditEnvironment,
# objectives
RegretMinimization,
# runner
OnlineRunner,
# algorithms
ThompsonSampling,
EpsilonGreedy,
UCB1,
RandomPolicy,
)
import matplotlib.pyplot as plt
env = BanditEnvironment(
n_arms=5,
arm_means=np.array([0.1, 0.3, 0.5, 0.4, 0.2]), # arm 3 is the best arm
seed=42,
)
policies = {
"Random": RandomPolicy(n_arms=5, seed=42),
"Greedy": EpsilonGreedy(n_arms=5, epsilon=0.0, seed=42),
"Epsilon-Greedy": EpsilonGreedy(n_arms=5, epsilon=0.1, seed=42),
"UCB1": UCB1(n_arms=5, seed=42),
"Thompson": ThompsonSampling(n_arms=5, seed=42),
}
objective = RegretMinimization(optimal_reward=0.5)
runner = OnlineRunner()
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
result = {}
# run each policy and plot
for name, policy in policies.items():
env.reset_rng(42)
result[name] = runner.run(policy, env, n_steps=1000, objective=objective)
print(
f"{name:15} | Final Regret: {result.final_regret:.2f} | Avg Reward: {result.average_reward:.3f}"
)
result[name].plot(metric="cumulative_regret", ax=axes[0], label=name)
result[name].plot(metric="average_reward", ax=axes[1], label=name)
axes[0].legend()
axes[0].set_title("Cumulative Regret Over Time")
axes[1].legend()
axes[1].set_title("Average Reward Over Time")
# Random | Final Regret: 194.00 | Avg Reward: 0.306
# Greedy | Final Regret: 103.00 | Avg Reward: 0.397
# Epsilon-Greedy | Final Regret: 28.00 | Avg Reward: 0.472
# UCB1 | Final Regret: 75.00 | Avg Reward: 0.425
# Thompson | Final Regret: 33.00 | Avg Reward: 0.467
links
papers
-
Armstrong, Kline, and Sun propose a general procedure to choose between a robustness (bias) and efficiency tradeoff. The basic idea is to use a known bound on the bias to shrink the unrestricted (robust, but inefficient) estimator toward a restricted (efficient, but potentially biased) estimator. This takes the form of a soft-thresholding estimator that is a smoothed version of a pre-test estimator (e.g. the F-test I propose to choose between the biased but efficient 2WFE estimator and the unbiased but high-variance full-interacted version here). This is a nice setup but I come away wondering how to elicit said bounds from applied researchers [the authors provide a shiny app that makes the computation straightforward once the bounds are known]. Related - Lepskii’s method applications in applied econometrics.
-
Waghmare and Ziegel is a nice review article on scoring rules for forecasting. For applications of these ideas to causal inference, see Zhao 2019, which proposes balancing weights based on minimizing covariate balancing scoring rules.
-
Li on ‘localizing’ empirical bayes methods for better performance when context is available. In EB applications to A/B test archives I’ve seen, one ends up pooling across extremely heterogeneous experiments (both in covariate space and time), which has always bothered me. This paper provides a nice way to address more local structure.
-
Feng et al set up choice models represented as a tree, which nests a wide variety of discrete choice models with random/data-dependent consideration sets.
-
Kato is a nice review paper outlining automatic debiased machine learning from the unifying perspective of Riesz representer estimation via Bregman divergence minimization.
-
Chen provides a nice didactic introduction to Variational Autoencoders and Diffusion Models from a statistical ML perspective.
-
course material for dynamic structural econometrics summer school
code, music
-
bit looks like a fun CLI tool to generate logos for programming projects. I find hex stickers played out and cringy, so clean ANSI art is more my speed.
-
filessh a file manager for ssh connections, looks useful.
-
new snarky puppy - audio engineers and technicians cower in fear at the sheer complexity of this setup.